
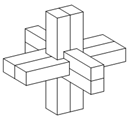
 ��ͼΪ�й���ͳ�������³��������Դ�ڹŴ����彨�����״����î�ṹ��������ά��ƴ�������ڲ��İ����֣����î�ṹ�����ϣ���ۿ�����˿�Ϸ��ʮ�������壬�����¡����ҡ�ǰ����ȫ�Գƣ�������ȫ��ͬ�����������ֳ����飬��90���î����������һ³���������������ĵ��������α߳�Ϊ1��������������������ڣ������ڵĺ�Ⱥ��Բ��ƣ����������������������СֵΪ30�У�������������ĸ�Ϊ��������
��ͼΪ�й���ͳ�������³��������Դ�ڹŴ����彨�����״����î�ṹ��������ά��ƴ�������ڲ��İ����֣����î�ṹ�����ϣ���ۿ�����˿�Ϸ��ʮ�������壬�����¡����ҡ�ǰ����ȫ�Գƣ�������ȫ��ͬ�����������ֳ����飬��90���î����������һ³���������������ĵ��������α߳�Ϊ1��������������������ڣ������ڵĺ�Ⱥ��Բ��ƣ����������������������СֵΪ30�У�������������ĸ�Ϊ��������| A�� | $2\sqrt{6}$ | B�� | $2\sqrt{7}$ | C�� | $4\sqrt{2}$ | D�� | 5 |
���� ��������������İ뾶����Сֵr=$\frac{\sqrt{30}}{2}$���Ӷ��õ�����������ĶԽ��߳�Ϊ$\sqrt{30}$���ɴ����������������ĸߣ�
��� �⣺�������������������СֵΪ30�У�
�����������İ뾶����СֵΪr=$\sqrt{\frac{30��}{4��}}$=$\frac{\sqrt{30}}{2}$��
������������ĶԽ��߳�Ϊ$\sqrt{30}$��
������������ĸ�Ϊh��
��12+12+h2=30��
���h=2$\sqrt{7}$��
��ѡ��B��
���� ���⿼�������������ĸߵȻ���֪ʶ������������֤����������������������麯���뷽��˼�롢������ת��˼�룬���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{{\sqrt{2}}}{2}$ | C�� | $\frac{{\sqrt{3}}}{2}$ | D�� | $\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com