
分析 求出A,B的坐标,代入三角形面积公式可得b与a,b的关系,根据离心率公式得出a,b的关系,从而可求出p的值.
解答 解:双曲线的渐近线方程为y=±$\frac{b}{a}x$,抛物线的准线方程为x=-$\frac{p}{2}$,
∴A(-$\frac{p}{2}$,$\frac{bp}{2a}$),B(-$\frac{p}{2}$,-$\frac{bp}{2a}$),
∴S△AOB=$\frac{1}{2}×\frac{p}{2}×\frac{bp}{a}$=$\frac{\sqrt{3}}{4}$,∴bp2=$\sqrt{3}$a,即p2=$\frac{\sqrt{3}a}{b}$.
∵e=$\frac{c}{a}=\frac{\sqrt{{a}^{2}+{b}^{2}}}{a}=2$,∴b2=3a2,即$\frac{a}{b}=\frac{\sqrt{3}}{3}$,
∴p2=$\frac{\sqrt{3}a}{b}$=1.
∴p=1.
故答案为1.
点评 本题考查了双曲线与抛物线的性质,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
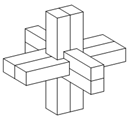 如图为中国传统智力玩具鲁班锁,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,六根完全相同的正四棱柱分成三组,经90°榫卯起来.现有一鲁班锁的正四棱柱的底面正方形边长为1,欲将其放入球形容器内(容器壁的厚度忽略不计),若球形容器表面积的最小值为30π,则正四棱柱体的高为( )
如图为中国传统智力玩具鲁班锁,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,六根完全相同的正四棱柱分成三组,经90°榫卯起来.现有一鲁班锁的正四棱柱的底面正方形边长为1,欲将其放入球形容器内(容器壁的厚度忽略不计),若球形容器表面积的最小值为30π,则正四棱柱体的高为( )| A. | $2\sqrt{6}$ | B. | $2\sqrt{7}$ | C. | $4\sqrt{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}+1}{2}$ | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\sqrt{3}$-1 | D. | $\frac{\sqrt{5}-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<1} | B. | {x|x≤2} | C. | {0,1} | D. | {1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com