
分析 由函数的奇偶性与周期性把f($\frac{1}{2}$)转化为求f($\frac{7}{2}$)的值求解.
解答 解:∵函数f(x)是定义在R上且周期为4的偶函数,
∴$f(\frac{1}{2})=f(-\frac{1}{2})=f(4-\frac{1}{2})=f(\frac{7}{2})$,
又当x∈[2,4]时,$f(x)=|lo{g}_{4}(x-\frac{3}{2})|$,
∴f($\frac{1}{2}$)=f($\frac{7}{2}$)=$|lo{g}_{4}(\frac{7}{2}-\frac{3}{2})|=|lo{g}_{4}2|=\frac{lg2}{lg4}=\frac{lg2}{2lg2}=\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查函数的周期性和奇偶性的应用,考查数学转化思想方法,是基础题.


科目:高中数学 来源: 题型:填空题
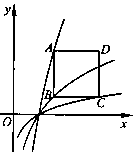 如图,已知正方形ABCD的边长为2,BC平行于x轴,顶点A,B和C分别在函数y1=3logax,y2=2logax和y3=logax(a>1)的图象上,则实数a的值为$\sqrt{2}$.
如图,已知正方形ABCD的边长为2,BC平行于x轴,顶点A,B和C分别在函数y1=3logax,y2=2logax和y3=logax(a>1)的图象上,则实数a的值为$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
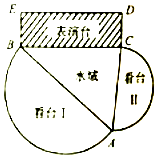 在水域上建一个演艺广场,演艺广场由看台Ⅰ,看台Ⅱ,三角形水域ABC,及矩形表演台BCDE四个部分构成(如图),看台Ⅰ,看台Ⅱ是分别以AB,AC为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍,矩形表演台BCDE 中,CD=10米,三角形水域ABC的面积为$400\sqrt{3}$平方米,设∠BAC=θ.
在水域上建一个演艺广场,演艺广场由看台Ⅰ,看台Ⅱ,三角形水域ABC,及矩形表演台BCDE四个部分构成(如图),看台Ⅰ,看台Ⅱ是分别以AB,AC为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍,矩形表演台BCDE 中,CD=10米,三角形水域ABC的面积为$400\sqrt{3}$平方米,设∠BAC=θ.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|1≤x<2} | C. | {x|1<x≤2} | D. | {x|1≤x≤2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com