
| 愿意被外派 | 不愿意被外派 | 合计 | |
| 70后 | 20 | 20 | 40 |
| 80后 | 40 | 20 | 60 |
| 合计 | 60 | 40 | 100 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
分析 (Ⅰ)计算观测值,对照临界值表即可得出结论;
(Ⅱ)用列表法求出所有基本事件数和愿意被外派人数不少于不愿意被外派人数的事件数,
从而计算所求的概率值.
解答 解:(Ⅰ)计算${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}=\frac{{100×{{(20×20-40×20)}^2}}}{60×40×60×40}=\frac{400×400×100}{5760000}$
≈2.778>2.706,
所以有90%以上的把握认为“是否愿意被外派与年龄有关”;
(Ⅱ)设70后员工中报名参加活动有愿意被外派的3人为Y1,Y2,Y3,
不愿意被外派的3人为N1,N2,N3,现从中选4人,
如图表所示,用×表示没有被选到,
| Y1 | Y2 | Y3 | N1 | N2 | N3 | |
| 1 | × | × | ||||
| 2 | × | × | ||||
| 3 | × | × | ||||
| 4 | × | × | ||||
| 5 | × | × | ||||
| 6 | × | × | ||||
| 7 | × | × | ||||
| 8 | × | × | ||||
| 9 | × | × | ||||
| 10 | × | × | ||||
| 11 | × | × | ||||
| 12 | × | × | ||||
| 13 | × | × | ||||
| 14 | × | × | ||||
| 15 | × | × |
点评 本题考查了独立性检验与列举法求古典概型的概率问题,是基础题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年龄 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 10 | 30 | 30 | 20 | 5 | 5 |
| 赞成人数 | 8 | 25 | 24 | 10 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
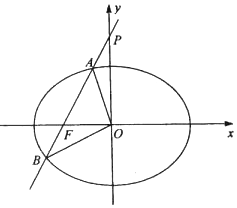 已知椭圆C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点为F(-1,0),左准线为x=-2.
已知椭圆C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点为F(-1,0),左准线为x=-2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若f(x)是奇函数,则f(x)是单调函数 | |
| B. | 命题“若x2-x-2=0,则x=1”的逆否命题是“若x≠1,则x2-x-2=0” | |
| C. | 命题p:?x∈R,2x>1024,则¬p:?x0∈R,${2^{x_0}}<1024$ | |
| D. | 命题“?x∈(-∞,0),2x<x2”是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | (¬p)∧(¬q) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com