
分析 (Ⅰ)直线l的参数方程为$\left\{\begin{array}{l}x=1+t\\ y=\sqrt{3}+\sqrt{3}t\end{array}$(t为参数).消去参数t可得直线l的普通方程.曲线C的极坐标方程为ρ2-4ρcosθ-2$\sqrt{3}$ρsinθ+4=0,利用互化公式可得:曲线C的直角坐标方程.
(Ⅱ)直线l的极坐标方程是$θ=\frac{π}{3}$,代入曲线C的极坐标方程得:ρ2-5ρ+4=0,可得|OA|•|OB|=|ρAρB|.
解答 解:(Ⅰ)直线l的参数方程为$\left\{\begin{array}{l}x=1+t\\ y=\sqrt{3}+\sqrt{3}t\end{array}$(t为参数).
消去参数t可得直线l的普通方程是$y-\sqrt{3}=\sqrt{3}(x-1)$,即$y=\sqrt{3}x$.
曲线C的极坐标方程为ρ2-4ρcosθ-2$\sqrt{3}$ρsinθ+4=0,
利用互化公式可得:曲线C的直角坐标方程是${x^2}+{y^2}-4x-2\sqrt{3}y+4=0$,即${(x-2)^2}+{(y-\sqrt{3})^2}=3$.
(Ⅱ)直线l的极坐标方程是$θ=\frac{π}{3}$,代入曲线C的极坐标方程得:ρ2-5ρ+4=0,
所以|OA|•|OB|=|ρAρB|=4.
点评 本题考查了极坐标化为直角坐标方程、参数方程化为普通方程、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 愿意被外派 | 不愿意被外派 | 合计 | |
| 70后 | 20 | 20 | 40 |
| 80后 | 40 | 20 | 60 |
| 合计 | 60 | 40 | 100 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,2) | C. | (-1,1] | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
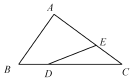
| A. | $\frac{3}{4}b-\frac{1}{3}a$ | B. | $\frac{5}{12}a-\frac{3}{4}b$ | C. | $\frac{3}{4}a-\frac{1}{3}b$ | D. | $\frac{5}{12}b-\frac{3}{4}a$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com