
分析 (1)曲线C的极坐标方程为ρ=6sinθ,即ρ2=6ρsinθ,利用互化公式可得直角坐标方程:x2+y2=6y,配方可得圆心C(0,3),半径r=3.直线l的参数方程为$\left\{\begin{array}{l}{x=1+at}\\{y=2+t}\end{array}\right.$(t为参数),消去参数t可得普通方程.
(2)由直线l经过定点P(1,2),此点在圆的内部,因此当CP⊥l时,|BD|取到最小值,利用相互垂直的直线斜率之间的关系可得k1,即可得出.
解答 解:(1)曲线C的极坐标方程为ρ=6sinθ,即ρ2=6ρsinθ,
化为直角坐标方程:x2+y2=6y,配方为:x2+(y-3)2=9,圆心C(0,3),半径r=3.
直线l的参数方程为$\left\{\begin{array}{l}{x=1+at}\\{y=2+t}\end{array}\right.$(t为参数),消去参数t可得:x-ay+2a-1=0.
(2)由直线l经过定点P(1,2),此点在圆的内部,
因此当CP⊥l时,|BD|取到最小值,则${k_{CP}}•{k_1}=\frac{2-3}{1-0}×{k_1}=-1$,解得k1=1.
∴$\frac{1}{a}=1$,解得a=1.
点评 本题考查了极坐标化为直角坐标方程、参数方程化为普通方程及其应用,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
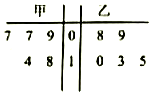 如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定(方差较小)的那名运动员的得分的方差为$\frac{34}{5}$.
如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定(方差较小)的那名运动员的得分的方差为$\frac{34}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年龄 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 10 | 30 | 30 | 20 | 5 | 5 |
| 赞成人数 | 8 | 25 | 24 | 10 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 10 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com