
分析 先根据数列的递推公式求出数列{an}的通项公式,即可得到数列{bn}的通项公式,裂项求和即可.
解答 解:∵数列{an}满足a1=1,an+1=$\frac{a_n}{{2{a_n}+1}}$(n∈N*),
∴$\frac{1}{{a}_{n+1}}$=$\frac{2{a}_{n}+1}{{a}_{n}}$=2+$\frac{1}{{a}_{n}}$,
∴$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=2,
∵$\frac{1}{{a}_{1}}$=1,
∴数列{$\frac{1}{{a}_{n}}$}是以1为首项,以2为公差的等差数列,
∴$\frac{1}{{a}_{n}}$=1+2(n-1)=2n-1,
∴bn=$\frac{a_n}{2n+1}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
∴数列{bn}的前n项和Sn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$,
故答案为:$\frac{n}{2n+1}$.
点评 本题考查了裂项求和和数列的递推公式,考查了学生的运算能力,属于中档题


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 愿意被外派 | 不愿意被外派 | 合计 | |
| 70后 | 20 | 20 | 40 |
| 80后 | 40 | 20 | 60 |
| 合计 | 60 | 40 | 100 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
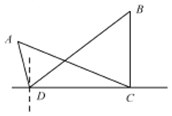 如图所示,为了测量A,B处岛屿的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为( )
如图所示,为了测量A,B处岛屿的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为( )| A. | $20\sqrt{6}$海里 | B. | $40\sqrt{6}$海里 | C. | $20(1+\sqrt{3})$海里 | D. | 40海里 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3-2\sqrt{2}$ | B. | 3 | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com