练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知圆的方程为，直线的方程为，点在直线上.

    （1）若点的坐标为，过点作圆的割线交圆于两点，当 时，求直线的方程；.

    （2）若过点作圆的切线，切点为，求证：经过四点的圆必过定点，并求出所有定点的坐标.

    【答案】（1）或；（2）过定点

    【解析】

    (1)依题意，先设直线方程y2=k(x-1)，由点到直线距离公式即可求解;

    (2)先由条件得到圆心坐标，写出圆的标准方程，化简整理，由圆的方程即可求出结果.

    解：(1)依题意，割线CD的斜率一定存在，设为k,则其方程为：y2=k(x-1)，

    即kx-y+2k=0.

    则圆心到直线的距离，且

    ∴直线CD的方程为：

    (2)由条件可知四点在以为直径的圆上，设

    又则的中点为所以经过四点的圆的方程为化简得

    由解得 或

    于是经过四点的圆必过定点

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】若平面直角坐标系内两点P，Q满足条件：①P，Q都在函数f(x)的图象上；②P，Q关于原点对称，则称点对(P，Q)是函数f(x)的图象上的一个“友好点对”(点对(P，Q)与点对(Q，P)看作同一个“友好点对”)．已知函数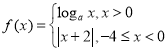，若此函数的“友好点对”有且只有一对，则实数的取值范围是_________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线的极坐标方程为，倾斜角为的直线过点.

    （1）求曲线的直角坐标方程和直线的参数方程；

    （2）设,是过点且关于直线对称的两条直线，与交于两点，与交于, 两点. 求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A＝{x|1≤x≤3}，B＝{x|x＞2}．

    （Ⅰ）分别求A∩B，（RB）∪A；

    （Ⅱ）已知集合C＝{x|1＜x＜a}，若CA，求实数a的取值集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设是两个非零平面向量，则有：

    ①若，则

    ②若，则

    ③若，则存在实数，使得

    ④若存在实数，使得，则或四个命题中真命题的序号为 __________．（填写所有真命题的序号）

    【答案】①③④

    【解析】逐一考查所给的结论：

    ①若，则，据此有：，说法①正确；

    ②若，取，则，

    而，说法②错误；

    ③若，则，据此有：，

    由平面向量数量积的定义有：，

    则向量反向，故存在实数，使得，说法③正确；

    ④若存在实数，使得，则向量与向量共线，

    此时，，

    若题中所给的命题正确，则，

    该结论明显成立.即说法④正确；

    综上可得：真命题的序号为①③④.

    点睛：处理两个向量的数量积有三种方法：利用定义；利用向量的坐标运算；利用数量积的几何意义．具体应用时可根据已知条件的特征来选择，同时要注意数量积运算律的应用．

    【题型】填空题
    【结束】
    17

    【题目】已知在中，，且.

    （1）求角的大小；

    （2）设数列满足，前项和为，若，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在R上的函数f（x）=3x．

    （1）若f（x）=8，求x的值；

    （2）对于任意的x∈[0，2]，[f（x）-3]3x+13-m≥0恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义域为，对任意、都有，当时，，.

    （1）求；

    （2）证明：在上单调递减；

    （3）解不等式：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在斜三棱柱中，侧面与侧面都是菱形，，．

    求证：；

    若，求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司订购了一批树苗，为了检测这批树苗是否合格，从中随机抽测 株树苗的高度，经数据处理得到如图的频率分布直方图，起中最高的 株树苗高度的茎叶图如图所示，以这 株树苗的高度的频率估计整批树苗高度的概率.

    （1）求这批树苗的高度高于 米的概率，并求图19-1中， ， ， 的值；

    （2）若从这批树苗中随机选取 株，记 为高度在 的树苗数列，求 的分布列和数学期望.

    （3）若变量 满足且 ，则称变量 满足近似于正态分布 的概率分布.如果这批树苗的高度满足近似于正态分布 的概率分布，则认为这批树苗是合格的，将顺利获得签收；否则，公司将拒绝签收.试问，该批树苗能否被签收？

    查看答案和解析>>

    同步练习册答案