
【题目】已知函数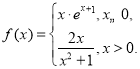 若关于
若关于![]() 的不等式
的不等式![]() 的解集非空,且为有限集,则实数
的解集非空,且为有限集,则实数![]() 的取值集合为___________.
的取值集合为___________.
【答案】![]()
【解析】
利用导数,研究![]() 的性质和图像;利用换元法,结合二次不等式的解集,结合
的性质和图像;利用换元法,结合二次不等式的解集,结合![]() 的函数图像,即可分类讨论求得.
的函数图像,即可分类讨论求得.
当![]() 时,
时,![]() ,则
,则![]() ,令
,令![]() ,解得
,解得![]() ,
,
容易得![]() 在区间
在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增,
单调递增,
且在![]() 时,取得极小值,即
时,取得极小值,即![]() ;且
;且![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,则
,则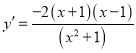 ,令
,令![]() ,解得
,解得![]() ,
,
容易得![]() 在区间
在区间![]() 单调递增,在区间
单调递增,在区间![]() 单调递减,
单调递减,
且在![]() 时,取得极大值,即
时,取得极大值,即![]() ;且
;且![]() 时,
时,![]() ;
;
故![]() 的模拟图像如下所示:
的模拟图像如下所示:
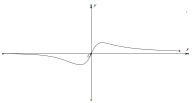
综上所述:![]() 的值域为
的值域为![]() .
.
令![]() ,则
,则![]() ,其
,其![]() ,对称轴为
,对称轴为![]() :
:
当![]() 时,显然关于
时,显然关于![]() 的二次不等式解集为空集,不满足题意;
的二次不等式解集为空集,不满足题意;
当![]() ,即
,即![]() 或
或![]() 时,
时,
若![]() ,显然关于
,显然关于![]() 的二次不等式的解集为
的二次不等式的解集为![]() ,又
,又![]() ,
,
数形结合可知,此时关于![]() 的原不等式解集为空集,不满足题意;
的原不等式解集为空集,不满足题意;
若![]() ,关于
,关于![]() 的二次不等式的解集为
的二次不等式的解集为![]() ,又
,又![]() ,
,
数形结合可知,此时关于![]() 的原不等式解集为
的原不等式解集为![]() ,满足题意;
,满足题意;
当![]() ,即
,即![]() 或
或![]() 时,
时,
令![]() ,解得
,解得![]() ,
,
显然![]() ,故此时关于
,故此时关于![]() 的不等式的解集为
的不等式的解集为![]() ,
,
数形结合可知,要满足题意,只需![]() 或
或![]() .
.
即![]() ,解得
,解得![]() ,满足
,满足![]() 或
或![]() ;
;
或![]() ,解得
,解得![]() ,不满足
,不满足![]() 或
或![]() ,舍去;
,舍去;
综上所述,要满足题意,则![]() 或
或![]() .
.
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】某商场进行有奖促销活动,顾客购物每满500元,可选择返回50元现金或参加一次抽奖,抽奖规则如下:从1个装有6个白球、4个红球的箱子中任摸一球,摸到红球就可获得100元现金奖励,假设顾客抽奖的结果相互独立.
(Ⅰ)若顾客选择参加一次抽奖,求他获得100元现金奖励的概率;
(Ⅱ)某顾客已购物1500元,作为商场经理,是希望顾客直接选择返回150元现金,还是选择参加3次抽奖?说明理由;
(Ⅲ)若顾客参加10次抽奖,则最有可能获得多少现金奖励?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市房产中心数据研究显示,2018年该市新建住宅销售均价如下表.3月至7月房价上涨过快,为抑制房价过快上涨,政府从8月份开始出台了相关限购政策,10月份开始房价得到了很好的抑制.
均价(万元/ | 0.95 | 0.98 | 1.11 | 1.12 | 1.20 | 1.22 | 1.32 | 1.34 | 1.16 | 1.06 |
月份 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
(Ⅰ)请建立3月至7月线性回归模型(保留小数点后3位),并预测若政府不宏观调控,12月份该市新建住宅销售均价;
(Ⅱ)试用相关系数说明3月至7月各月均价![]() (万元/
(万元/![]() )与月份
)与月份![]() 之间可用线性回归模型(保留小数点后2位)
之间可用线性回归模型(保留小数点后2位)
参考数据:![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
回归方程斜率和截距最小二乘法估计公式 ;
;
相关系数 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的短轴长为2,直线
的短轴长为2,直线![]() 被椭圆截得的线段长为
被椭圆截得的线段长为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() ,与椭圆交于
,与椭圆交于![]() 、
、![]() 两点时,作线段
两点时,作线段![]() 的垂直平分线分别交
的垂直平分线分别交![]() 轴、
轴、![]() 轴于
轴于![]() 、
、![]() ,垂足为
,垂足为![]() ,使得
,使得![]() 与
与![]() 的面积相等,若存在,试求出直线
的面积相等,若存在,试求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年,新冠状肺炎疫情牵动每一个中国人的心,危难时刻众志成城,共克时艰,为疫区助力.福建省漳州市东山县共101个海鲜商家及个人为缓解武汉物质压力,募捐价值百万的海鲜输送武汉.东山岛,别称陵岛,形似蝴蝶亦称蝶岛,隶属于福建省漳州市东山县,是福建省第二大岛,中国第七大岛,介于厦门市和广东省汕头之间,东南是著名的闽南渔场和粤东渔场交汇处,因地理位置发展海产品养殖业具有得天独厚的优势.根据养殖规模与以往的养殖经验,某海鲜商家的海产品每只质量(克)在正常环境下服从正态分布![]() .
.
(1)随机购买10只该商家的海产品,求至少买到一只质量小于265克该海产品的概率;
(2)2020年该商家考虑增加先进养殖技术投入,该商家欲预测先进养殖技术投入为49千元时的年收益增量.现用以往的先进养殖技术投入![]() (千元)与年收益增量
(千元)与年收益增量![]() (千元).
(千元).![]() 的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线
的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线![]() 的附近,且
的附近,且![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() ,其中
,其中![]()
![]() .根据所给的统计量,求y关于x的回归方程,并预测先进养殖技术投入为49千元时的年收益增量.
.根据所给的统计量,求y关于x的回归方程,并预测先进养殖技术投入为49千元时的年收益增量.
附:若随机变量![]() ,则
,则![]()
![]() ;
;
对于一组数据![]()
![]()
![]()
![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为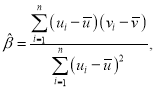
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() .(
.(![]() 为参数)以坐标原点
为参数)以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标和 l的直角坐标方程;
的直角坐标和 l的直角坐标方程;
(2)把曲线![]() 上各点的横坐标伸长为原来的
上各点的横坐标伸长为原来的![]() 倍,纵坐标伸长为原来的
倍,纵坐标伸长为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,
,![]() 为
为![]() 上动点,求
上动点,求![]() 中点
中点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 经过点
经过点![]() 且倾斜角为
且倾斜角为![]() .
.
(1)求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,满足
,满足![]() 为
为![]() 的中点,求
的中点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() ,点
,点![]() ,动圆
,动圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 相切于点
相切于点![]() (
(![]() 均不同于点
均不同于点![]() ),且
),且![]() 与
与![]() 交于点
交于点![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)证明:![]() 为定值,并求
为定值,并求![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 两点,当
两点,当![]() 三点共线时,求四边形
三点共线时,求四边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com