Question

4．棱长为1的正四面体的四个面的中心所组成的小四面体的外接球的体积为$\frac{\sqrt{6}}{216}$π．

Answer 1

分析 由于原正四面体的棱长为1，由此可得BD=1，由中位线定理可知：GH=$\frac{1}{2}$BD=$\frac{1}{2}$，又由重心定理可知：EF=$\frac{2}{3}$GH=$\frac{1}{3}$，小四面体放于正方体内，正方体的边长为$\frac{1}{3\sqrt{2}}$，对角线长为$\frac{1}{\sqrt{6}}$，外接球的半径为$\frac{1}{2\sqrt{6}}$，由此可得体积．

解答 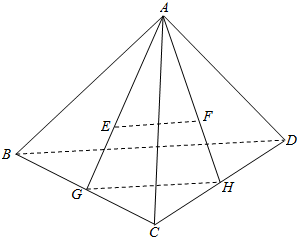解：如图，设G，H分别是BC，CD的中点，E，F分别是三角形ABC，ACD的重心，BD=1，
由中位线定理可知：GH=$\frac{1}{2}$BD=$\frac{1}{2}$，
又由重心定理可知：EF=$\frac{2}{3}$GH=$\frac{1}{3}$，
小四面体放于正方体内，正方体的边长为$\frac{1}{3\sqrt{2}}$，
对角线长为$\frac{1}{\sqrt{6}}$，外接球的半径为$\frac{1}{2\sqrt{6}}$，
体积为$\frac{4}{3}$π（$\frac{1}{2\sqrt{6}}$）³=$\frac{\sqrt{6}}{216}$π．
故答案为：$\frac{\sqrt{6}}{216}$π．

点评 本小题主要考查棱锥的结构特征，球的体积等基本知识，同时考查空间想象能力和推理、运算能力，属于中档题．