
| A. | $2\sqrt{2}$ | B. | $2\sqrt{5}$ | C. | $\sqrt{17}$ | D. | $\sqrt{15}$ |
分析 利用向量的数量积运算即可得出.
解答 解:向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$-$\overrightarrow{b}$=(${\sqrt{3}$,$\sqrt{2}}$),
可得|$\overrightarrow{a}$-$\overrightarrow{b}$|2=5,即|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2-2$\overrightarrow{a}$•$\overrightarrow{b}$=5,解得$\overrightarrow{a}$•$\overrightarrow{b}$=0.
|$\overrightarrow{a}$+2$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+4|$\overrightarrow{b}$|2-4$\overrightarrow{a}$•$\overrightarrow{b}$=1+16=17.
|$\overrightarrow{a}$+2$\overrightarrow{b}$|=$\sqrt{17}$.
故选:C.
点评 熟练掌握向量的数量积运算是解题的关键.


科目:高中数学 来源: 题型:选择题
| A. | f(b)<f(a)<f(c) | B. | f(c)<f(b)<f(a) | C. | f(c)<f(a)<f(b) | D. | f(b)<f(c)<f(a) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,5)∈M | B. | (1,5)∈M | C. | (-1,1)∈M | D. | -1∈M |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
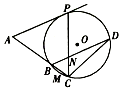 如图,过点A分别作⊙O的切线AP与割线AC,P为切点,AC与⊙O交于B,C两点,圆心O在∠PAC的内部,BD∥AP,PC与BD交于点N.
如图,过点A分别作⊙O的切线AP与割线AC,P为切点,AC与⊙O交于B,C两点,圆心O在∠PAC的内部,BD∥AP,PC与BD交于点N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(3,+∞) | B. | (-1,2] | C. | (-∞,2]∪(3,+∞) | D. | [-2,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(2,+∞) | B. | (-1,2) | C. | (-∞,$\frac{2}{3}$) | D. | (-∞,-2)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22 | B. | 48 | C. | $\sqrt{46}$ | D. | 32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com