
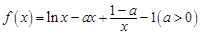 .
.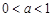 ,试讨论
,试讨论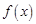 单调性;
单调性;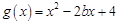 ,当
,当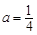 时,若
时,若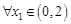 ,存在
,存在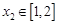 ,使
,使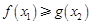 ,求实数
,求实数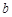 的
的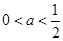 时,
时,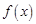 在
在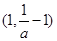 上是增函数,在
上是增函数,在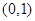 和
和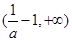 上是减函数;当
上是减函数;当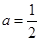 时,
时,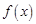 在
在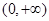 上是减函数;当
上是减函数;当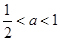 时,
时,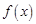 在
在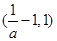 上是增函数,在
上是增函数,在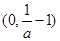 和
和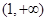 上是减函数;(2)
上是减函数;(2)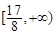 .
.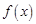 的导数,
的导数,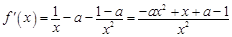 ,然后在
,然后在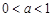 的范围内讨论
的范围内讨论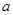 的大小以确定
的大小以确定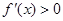 和
和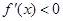 的解集;(2)
的解集;(2)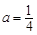 时,代入结合上问可知函数
时,代入结合上问可知函数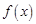 在在
在在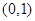 上是减函数,在
上是减函数,在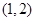 上是增函数,即在
上是增函数,即在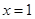 取最小值,若
取最小值,若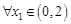 ,存在
,存在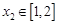 ,使
,使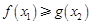 ,即存在
,即存在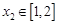 使得
使得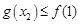 .从而得出实数
.从而得出实数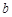 的取值范围.注意
的取值范围.注意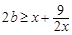 不能用基本不等式,因为
不能用基本不等式,因为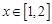 等号取不到,实际上
等号取不到,实际上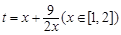 为减函数.所以其值域为
为减函数.所以其值域为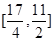 ,从而
,从而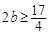 ,即有
,即有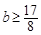 .
.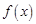 的定义域为
的定义域为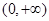 ,
,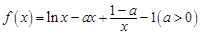 ,所以
,所以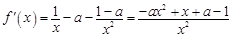 ,
,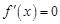 ,可得
,可得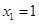 ,
,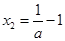 ,
,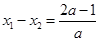 2分
2分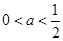 时,由
时,由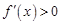 可得
可得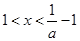 ,故此时函数
,故此时函数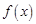 在
在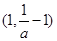 上是增函数.
上是增函数.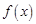 在
在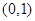 和
和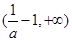 上是减函数. 4分
上是减函数. 4分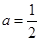 时,
时,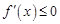 恒成立,故此时函数
恒成立,故此时函数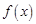 在
在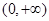 上是减函数. 6分
上是减函数. 6分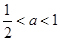 时,由
时,由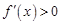 可得
可得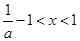 ,故此时函数
,故此时函数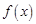 在
在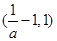 上是增函数,
上是增函数,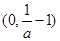 和
和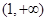 上是减函数; 8分
上是减函数; 8分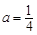 时,由(1)可知
时,由(1)可知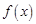 在
在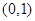 上是减函数,在
上是减函数,在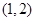 上是增函数,
上是增函数,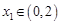 ,有
,有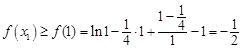 ,
,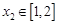 ,使
,使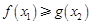 ,所以
,所以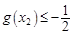 , 12分
, 12分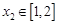 ,使得
,使得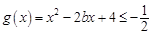 ,
,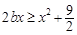 在
在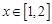 时有解,
时有解,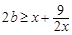 在
在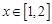 时有解,
时有解,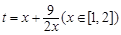 为减函数,故其值域为
为减函数,故其值域为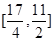 ,
,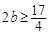 ,即有
,即有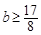 ,所以实数
,所以实数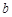 的取值范围是
的取值范围是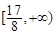 . 16分
. 16分

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:不详 题型:解答题
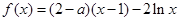 ,
,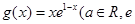 为自然对数的底数).
为自然对数的底数).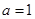 时,求
时,求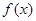 的单调区间;
的单调区间;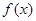 在
在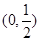 上无零点,求
上无零点,求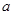 最小值;
最小值;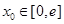 ,在
,在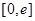 上总存在两个不同的
上总存在两个不同的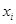
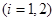 ),使
),使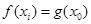 成立,求
成立,求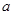 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com