练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数y＝f(x)，x∈D，若存在常数C，对任意的x1∈D，存在唯一的x2∈D使得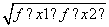＝C，则称函数f(x)在D上的几何平均数为C.已知f(x)＝x3，x∈[1,2]，则函数f(x)＝x3在[1,2]上的几何平均数为(　　)

    A.                            B．2

    C．4                              D．2


    D　令x1x2＝m，且1≤x1≤2,1≤x2≤2，则x2≤x1x2≤2x2，即x2≤m≤2x2，∴，可得m＝2，故C＝＝＝＝2.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图，四边形ABCD是正方形，E是AD上一点，且AE＝AD，N是AB的中点，

    NF⊥CE于F，求证：FN2＝EF·FC.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝|ax＋1|(a∈R)，不等式f(x)≤3的解集为{x|－2≤x≤1}．

    (1) 求a的值，

    (2) 若≤k恒成立，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知在递增等差数列{an}中，a1＝2，a1，a3，a7成等比数列，{bn}的前n项和为Sn，且Sn＝2n＋1－2.

    (1)求数列{an}、{bn}的通项公式；

    (2)设cn＝abn，求数列{cn}的前n项和Tn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知e1，e2是两个单位向量，其夹角为θ，若向量m＝2e1＋3e2，则|m|＝1的充要条件是(　　)

    A．θ＝π                         B．θ＝

    C．θ＝                         D．θ＝

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝ax＋b(0≤x≤1)，则a＋2b＞0是f(x)＞0在[0,1]上恒成立的________条件．(填充分但不必要，必要但不充分，充要，既不充分也不必要)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)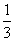＝x3－ax2－ax，g(x)＝2x2＋4x＋c.

    (1)试问函数f(x)能否在x＝－1时取得极值？说明理由；

    (2)若a＝－1，当x∈[－3,4]时，函数f(x)与g(x)的图象有两个公共点，求c的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝sin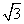＋cos ωx(其中ω＞0)，且函数f(x)的图象的两条相邻的对称轴间的距离为.

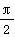    (1)求ω的值；

    (2)将函数y＝f(x)的图象上各点的横坐标伸长到原来的2倍，纵坐标不变，得到函数y＝g(x)的图象，求函数g(x)在区间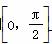上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


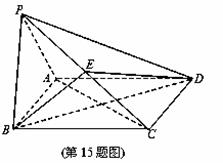
    如图，在四棱锥P－ABCD中，底面ABCD为矩形，平面PAB⊥平面ABCD，PA⊥PB， BP＝BC，E为PC的中点．

    （1）求证：AP∥平面BDE；

    （2）求证：BE⊥平面PAC．

    查看答案和解析>>

    同步练习册答案