
���� ��I��{an}�ǹ���Ϊ2�ĵȲ����У��������ʽ���ɵó�Sn��
��II����q��ʾ��$\sum_{k=1}^{n+1}$|bk|��4|bn|������q�ķ�Χ�����ʽ�ó�q-2=0��
��III�����������ɵ�{an}��{bn}��ͨ����Sm+1��4bm���Ӷ��ó�m�Ĵ����ԣ�
��� �⣺��I���ߣ�an+1-an��2=4��an+1��an����an+1-an=2��
��{an}����a1=1Ϊ�����2Ϊ����ĵȲ����У�
��an=1+2��n-1��=2n-1��
��Sn=$\frac{{a}_{1}+{a}_{n}}{2}��n$=n2��
��II����|bn+1|=q|bn|����|bn|=q|bn-1|=q2|bn-2|=qn-1|b1|=qn-1��
$\sum_{k=1}^{n+1}$|bk|=1+q+q2+��+qn=$\frac{1-{q}^{n+1}}{1-q}$��
�߳���q��1�Ҷ������n��N*������$\sum_{k=1}^{n+1}$|bk|��4|bn|��
��$\frac{1-{q}^{n+1}}{1-q}$��4qn-1����1-qn+1��4qn-1-4qn��
��qn-1��q2-4q+4����1����qn-1��q-2��2��1�������
��q=2��
��III���ɣ�II����֪{|bn|}����1Ϊ�����2Ϊ���ȵĵȱ����У�
��Tm��0����{bn}����1Ϊ�����2Ϊ���ȵĵȱ����У���bn=2n-1��
�ߣ�an+1-an��2=4����an+1-an=2��an+1-an=-2��
�ߴ���Ψһ������p��ֵ����ap��ap-1��
�൱n��p-1��n��pʱ��{an}�ǹ���Ϊ2�ĵ������У�
��p��2��
����p=2����an=$\left\{\begin{array}{l}{1��n=1}\\{2n-5��n��2}\end{array}\right.$����Sm=��m-2��2��
��Sm+1=��m-1��2����4bm=4•2m-1=2m+1��
��4bm-Sm+1=2m+1-��m-1��2��0��
��������ѧ���ɷ�����֤����
��m=1ʱ��������Ȼ������
����m=kʱ�����۳�������2k+1-��k-1��2��0��
��2k+2-k2��2•2k+1-��k-1��2��2k+1-��k-1��2��0��
����m=k+1ʱ������Ҳ������
��4bm-Sm+1��0���������������������mʹ��Sm+1=4bm��
����p��3����a1=1��a2=3��
��S2=1+3=4=4b1��
��P��3ʱ������������m=1��ʹ��Sm+1=4bm��
���ϣ���p=2ʱ��������������mʹ��Sm+1=4bm��
��p��3ʱ������������mʹ��Sm+1=4bm����ʱm=1��
���� ���⿼���˵Ȳ����С��ȱ����е����ʣ����еĵ������жϣ������е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=g��x������С������Ϊ�� | B�� | y=g��x����ͼ�����ֱ��x=$\frac{��}{6}$�Գ� | ||
| C�� | y=g��x����[-$\frac{��}{6}$��$\frac{��}{3}$]�ϵ������� | D�� | y=g��x����ͼ����ڵ㣨$\frac{5��}{12}$��0���Գ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{49}$ | B�� | 49 | C�� | $\frac{1}{7}$ | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
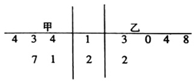 2017��3��2����16�գ�ȫ�������ڱ����ٿ����ס������н�5��������������ͳ����ͼ��ʾ����ס��ҵ�����ƽ�����ֱ�Ϊ$\overline{{x}_{1}}$��$\overline{{x}_{2}}$����λ���ֱ�Ϊy1��y2��������
2017��3��2����16�գ�ȫ�������ڱ����ٿ����ס������н�5��������������ͳ����ͼ��ʾ����ס��ҵ�����ƽ�����ֱ�Ϊ$\overline{{x}_{1}}$��$\overline{{x}_{2}}$����λ���ֱ�Ϊy1��y2��������| A�� | $\overline{{x}_{1}}$��$\overline{{x}_{2}}$��y1��y2 | B�� | $\overline{{x}_{1}}$��$\overline{{x}_{2}}$��y1=y2 | C�� | $\overline{{x}_{1}}$��$\overline{{x}_{2}}$��y1=y2 | D�� | $\overline{{x}_{1}}$��$\overline{{x}_{2}}$��y1��y2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com