
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
分析 本题是一个等可能事件的概率,试验发生包含的事件是在区间[0,1]上任取两个数a和b,写出事件对应的集合,做出面积,满足条件的事件是关于x的方程x2+2ax+b2=0有实数根,根据二次方程的判别式写出a,b要满足的条件,写出对应的集合,做出面积,得到概率.
解答 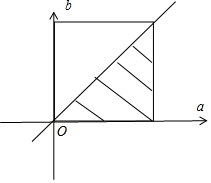 解:由题意知本题是一个等可能事件的概率,
解:由题意知本题是一个等可能事件的概率,
∵试验发生包含的事件是在区间[0,1]上任取两个数a和b,
事件对应的集合是Ω={(a,b)|0≤a≤1,0≤b≤1}
对应的面积是sΩ=1
满足条件的事件是关于x的方程x2+2ax+b2=0有实数根,
即4a2-4b2≥0,
∴a≥b,
事件对应的集合是A={(a,b)|0≤a≤1,0≤b≤1,a≥b}
对应的图形的面积是sA=$\frac{1}{2}$,
∴根据等可能事件的概率得到P=$\frac{1}{2}$.
故选C.
点评 本题考查几何概型,古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积的比值得到.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
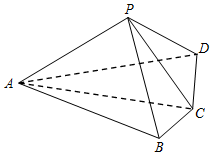 如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.
如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,∠GDC=90°,点E是线段GC的中点.
如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,∠GDC=90°,点E是线段GC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com