
| a |
| 3 |
| b |
| a |
| b |
| π |
| 4 |
| a |
| b |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
| a |
| b |
| 3 |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |


科目:高中数学 来源: 题型:
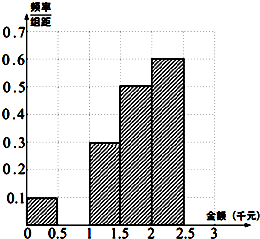 某青少年研究中心为了统计某市青少年(18岁以下)2014年春节所收压岁钱的情况进而研究青少年的消费去向,随机抽查了该市60名青少年所收压岁钱的情况,得到如下数据统计表:
某青少年研究中心为了统计某市青少年(18岁以下)2014年春节所收压岁钱的情况进而研究青少年的消费去向,随机抽查了该市60名青少年所收压岁钱的情况,得到如下数据统计表:| 压岁钱(单位:千元) | 频数 | 频率 |
| (0,0.5] | 3 | 0.05 |
| (0.5,1] | x | p |
| (1,1.5] | 9 | 0.15 |
| (1.5,2] | 15 | 0.25 |
| (2,2.5] | 18 | 0.30 |
| (2.5,3] | y | q |
| 合计 | 60 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
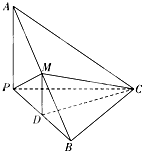 如图,已知三棱锥A-BPC中,AP⊥PC,PC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,PC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 2 |
| π |
| e |
| π |
| e |
| e |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com