
分析 (1)当a=-1 时,求出A,即可求A∩B.
(2)若A⊆B,确定A≠∅,再求实数a的取值范围.
解答 解:(1)当a=-1时,A=($\frac{1}{2}$,2],∴A∩B=($\frac{1}{2}$,2)…(5)
(2)∵A=(-$\frac{a}{2}$,$\frac{3-a}{2}$],A⊆B,
∴A=∅,-$\frac{a}{2}$≥$\frac{3-a}{2}$,不成立….…(7)
$\left\{\begin{array}{l}{-\frac{a}{2}≥-\frac{1}{2}}\\{\frac{3-a}{2}<2}\end{array}\right.$解,得:-1<a≤1.…(12)
点评 本题考查集合的运算与关系,考查学生的计算能力,比较基础.


 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 101 | B. | 122 | C. | 145 | D. | 170 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 大衍数列,来源于中国古代著作《乾坤谱》中对易传“大衍之数五十”的推论.其前10项为:0、2、4、8、12、18、24、32、40、50.
大衍数列,来源于中国古代著作《乾坤谱》中对易传“大衍之数五十”的推论.其前10项为:0、2、4、8、12、18、24、32、40、50.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
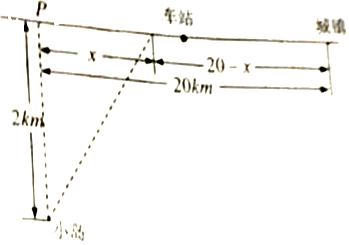
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{1}{5}$ | C. | 5 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{2}}}{5}$ | B. | $\frac{{\sqrt{2}}}{5}$ | C. | $-\frac{{\sqrt{2}}}{10}$ | D. | $\frac{{\sqrt{2}}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com