
分析 (1)利用){an}是递增数列,且a1,2a2,3a3成等差数列,得到关于p的方程解之;
(2)将p代入,利用累加法得到数列{an}的通项公式;
(3)由p=1得到|an+1-an|=1,而a1=1,得到后面的各项,观察分析规律,找到满足满足Sn=n的各项.
解答 解:(1){an}是递增数列,且a1,2a2,3a3成等差数列,4a2=a1+3a3,又a2-a1=p,a3-a2=p2,所以3p2-p=0,解得p=$\frac{1}{3}$或者p=0(舍去)
(2)p=$\frac{1}{2}$,且{a2n-1}是递增数列,{a2n}是递减数列,所以a2n-a2n-1>0,a2n+1-a2n<0,
${a}_{2n}-{a}_{2n-1}=(\frac{1}{2})^{2n-1}$,${a}_{2n+1}-{a}_{2n}=-(\frac{1}{2})^{2n}$,
所以an=a1+(a2-a1)+(a3-a2)+…(an-an-1)=1$+\frac{1}{2}$-$\frac{1}{{2}^{2}}$+…+$\frac{(-1)^{n}}{{2}^{n-1}}$=$\frac{4}{3}+\frac{1}{3}×\frac{(-1)^{n}}{{2}^{n-1}}$;
(3)由题意得|an+1-an|=1,而a1=1,
所以a2=2,0;a3=3,1,-1;a4=4,2,0,-2…
所以S1=1,S2=3,1;S3=6,4,2,0;S4=10,8,6,4,0,-2…
即S4k-3为奇数;S4k-2为偶数;S4k为偶数;因此只有S4k-3,S4k满足Sn=n.
点评 本题考查了数列求和以及数列递推关系的运用;属于难题.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
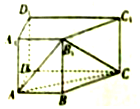 如图,在直四棱柱ABCD-A1B1C1D1中,AB∥DC,AA1=1,AB:AD:BC:DC=3:4:5:6,侧棱AA1⊥底面ABCD.
如图,在直四棱柱ABCD-A1B1C1D1中,AB∥DC,AA1=1,AB:AD:BC:DC=3:4:5:6,侧棱AA1⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{5}{6}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在统计学中,独立性检验是检验两个分类变量是否有关系的一种统计方法 | |
| B. | 在残差图中,残差分布的带状区域的宽度越狭窄,其模拟的效果越好 | |
| C. | 线性回归方程对应的直线$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$至少经过其样本数据点中的一个点 | |
| D. | 在回归分析中,相关指数R2越大,模拟的效果越好 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | tan$\frac{4π}{7}$>tan$\frac{3π}{7}$ | B. | tan$\frac{2π}{5}$<tan$\frac{3π}{5}$ | ||
| C. | tan(-$\frac{13π}{7}$)>tan(-$\frac{15π}{8}$) | D. | tan(-$\frac{13π}{4}$)<tan(-$\frac{12π}{5}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com