
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | $\frac{5}{4}$ |
分析 由已知求得$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$,结合$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,$\overrightarrow{a}$•$\overrightarrow{b}$=0得到关于k的一次方程得答案.
解答 解:由题意可得,$|\overrightarrow{{e}_{1}}|=|\overrightarrow{{e}_{2}}|=1$,$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}=|\overrightarrow{{e}_{1}}||\overrightarrow{{e}_{2}}|cos\frac{2π}{3}=-\frac{1}{2}$,
又$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,且$\overrightarrow{a}$•$\overrightarrow{b}$=0,
得$(\overrightarrow{{e}_{1}}-2\overrightarrow{{e}_{2}})•(k\overrightarrow{{e}_{1}}+\overrightarrow{{e}_{2}})$=$k|\overrightarrow{{e}_{1}}{|}^{2}+(1-2k)\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}-2|\overrightarrow{{e}_{2}}|=0$,
∴k$-\frac{1}{2}$(1-2k)-2=0,得k=$\frac{5}{4}$.
故选:D.
点评 本题考查平面向量的数量积运算,考查了计算能力,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 91种 | B. | 90种 | C. | 89种 | D. | 86种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,0) | B. | $(\frac{π}{3},0)$ | C. | $(\frac{π}{6},0)$ | D. | $(\frac{π}{9},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
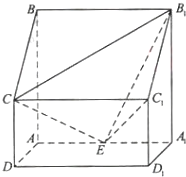 如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com