
【题目】我国是世界上严重缺水的归家之一,某市为了制订合理的节水方案,对家庭用水情况进行了抽样调查,获得了某年100个家庭的月均用水量(单位:![]() )的数据,将这些数据按照
)的数据,将这些数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
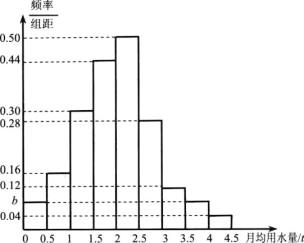
(1)求图中的![]() 值,若该市有30万个家庭,试估计全市月均用水量不低于
值,若该市有30万个家庭,试估计全市月均用水量不低于![]() 的家庭数;
的家庭数;
(2)假设同组中的每个数据都用该组区间的中点值代替,试估计全市家庭月均用水量的平均数;
(3)现从月均用水量在![]() ,
,![]() 的家庭中,先按照分层抽样的方法抽取9个家庭,再从这9家庭中抽取4个家庭,记这4个家庭中月均用水量在
的家庭中,先按照分层抽样的方法抽取9个家庭,再从这9家庭中抽取4个家庭,记这4个家庭中月均用水量在![]() 中的数量为
中的数量为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(1)![]() ,36000;(2)2.02;(3)分布列见解析,
,36000;(2)2.02;(3)分布列见解析,![]()
【解析】
(1)由题意![]() ,解得
,解得![]() ,由此可得全市月均用水量不低于
,由此可得全市月均用水量不低于![]() 的家庭所占比例为12%,从而求出答案;
的家庭所占比例为12%,从而求出答案;
(2)直接根据平均数的计算公式求解即可;
(3)按照分层抽样抽取9个家庭,即![]() 抽3家,
抽3家,![]() 抽6家,因此
抽6家,因此![]() 可能的取值为1,2,3,4,根据概率计算公式即可求出
可能的取值为1,2,3,4,根据概率计算公式即可求出![]() 的分布列,再根据期望的计算公式即可求出期望.
的分布列,再根据期望的计算公式即可求出期望.
解:(1)∵频率分布直方图中所有矩形的面积之和为1,
∴![]() ,解得
,解得![]() ,
,
∴月均用水量不低于![]() 的家庭所占比例
的家庭所占比例![]()
![]() ,
,
因此估计全市月均用水量不低于![]() 的家庭所占比例为12%,
的家庭所占比例为12%,
家庭数约为![]() ;
;
(2)因为![]()
![]()
![]()
![]()
![]() ,
,
因此估计全市家庭月均用水量的平均数为2.02;
(3)在月均用水量![]() ,
,![]() 中,
中,![]() 有4家,
有4家,![]() 有8家,共12家,
有8家,共12家,
按照分层抽样抽取9个家庭,即![]() 抽3家,
抽3家,![]() 抽6家,
抽6家,
因此![]() 可能的取值为1,2,3,4,
可能的取值为1,2,3,4,
其中![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() 的分布列如下表所示:
的分布列如下表所示:
| 1 | 2 | 3 | 4 |
|
|
|
|
|
数学期望![]() .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:
【题目】从某地区小学的期末考试中抽取部分学生的数学成绩,由抽查结果得到如图的频率分布直方图,分数落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
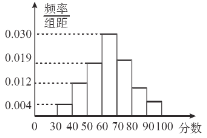
(1)求这些学生的分数落在区间![]() 内的频率;
内的频率;
(2)若将频率视为概率,从该地区小学的这些学生中随机抽取3人,记这3人中成绩位于区间![]() 内的人数为
内的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我国瓷器的历史上六棱形的瓷器非常常见,因为六,八是中国人的吉利数字,所以好多器都做成六棱形和八棱形,数学李老师有一个正六棱柱形状的笔筒,底面边长为6cm,高为18cm(底部及筒壁厚度忽略不计),一长度为![]() cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,底面ABCD为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,且平面
,且平面![]() 平面ABCD.
平面ABCD.
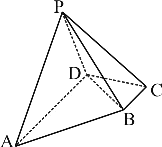
(1)求证:![]() ;
;
(2)在线段PA上是否存在一点M,使二面角M-BC-D的大小为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,分别过
有且仅有一个公共点,分别过![]() 两点作
两点作![]() ,垂足分别为
,垂足分别为![]() ,且记
,且记![]() 为点
为点![]() 到直线
到直线![]() 的距离,
的距离, ![]() 为点
为点![]() 到直线
到直线![]() 的距离,
的距离,![]() 为点
为点![]() 到点
到点![]() 的距离,试探索
的距离,试探索![]() 是否存在最大值.若存在,求出最大值;若不存在,请说明理由.
是否存在最大值.若存在,求出最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学有教师400人,其中高中教师240人.为了了解该校教师每天课外锻炼时间,现利用分层抽样的方法从该校教师中随机抽取了100名教师进行调查,统计其每天课外锻炼时间(所有教师每天课外锻炼时间均在![]() 分钟内),将统计数据按
分钟内),将统计数据按![]() ,
,![]() ,
,![]() ,…,
,…,![]() 分成6组,制成频率分布直方图如下:
分成6组,制成频率分布直方图如下:
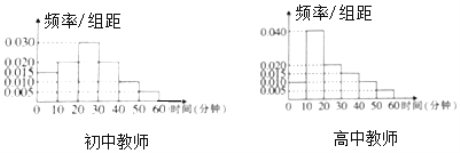
假设每位教师每天课外锻炼时间相互独立,并称每天锻炼时间小于20分钟为缺乏锻炼.
(1)试估计本校教师中缺乏锻炼的人数;
(2)若从参与调查,且每天课外锻炼时间在![]() 内的该校教师中任取2人,求至少有1名初中教师被选中的概率.
内的该校教师中任取2人,求至少有1名初中教师被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请从下面三个条件中任选一个,补充在下面的横线上,并作答.
①AB⊥BC,②FC与平面ABCD所成的角为![]() ,③∠ABC
,③∠ABC![]() .
.
如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,PA⊥平面ABCD,且PA=AB=2,,PD的中点为F.
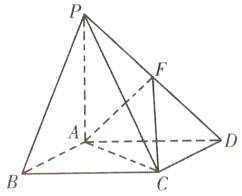
(1)在线段AB上是否存在一点G,使得AF![]() 平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
(2)若_______,求二面角F﹣AC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学一班级1999级同学举行20周年聚会,该班共来了12位同学,其中女同学6位,聚会过程中有一个游戏环节,在游戏环节中,需要随机从中选出2位同学代表,进行男女搭配完成该项游戏,因此,每次选出的2位同学是一男一女,才算“有效选择”;否则视为“无效选择”,继续下一次选择,直到成为“有效选择”为止.
(1)求第一次随机选出的2位同学是“有效选择”的概率;
(2)设第一次选出的2位同学代表中女同学人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com