
根据下列条件,求圆的方程.
(1)圆心在原点且圆周被直线3x+4y+15=0分成12两部分的圆的方程;
(2)求经过两已知圆C1x2+y2-4x+2y=0与C2x2+y2-2y-4=0的交点,且圆心在直线l2x+4y=1上的圆的方程.
科目:高中数学 来源: 题型:
如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC.∠ABC=45°,AB=2 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.
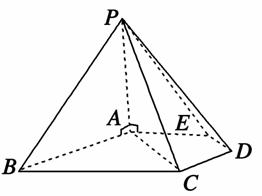
(1)求证:平面PCD⊥平面PAC;
(2)求直线PB与平面PCD所成角的大小;
(3)求四棱锥P-ACDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(1)若l在两坐标轴上的截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市石景山区高三上学期期末考试文科数学试卷(解析版) 题型:解答题
(本小题共13分)某校有150名学生参加了中学生环保知识竞赛,为了解成绩情况,现从中随机抽取50名学生的成绩进行统计(所有学生成绩均不低于60分).请你根据尚未完成的频率分布表,解答下列问题:
分组 | 频数 | 频率 | |
第1组 | [60,70) | M | 0.26 |
第2组 | [70,80) | 15 | p |
第3组 | [80,90) | 20 | 0.40 |
第4组 | [90,100] | N | q |
合计 | 50 | 1 | |
(Ⅰ)写出M 、N 、p、q(直接写出结果即可),并作出频率分布直方图;

(Ⅱ)若成绩在90分以上的学生获得一等奖,试估计全校所有参赛学生获一等奖的人数;
(Ⅲ)现从所有一等奖的学生中随机选择2名学生接受采访,已知一等奖获得者中只有2名女生,求恰有1名女生接受采访的概率.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市石景山区高三上学期期末考试理科数学试卷(解析版) 题型:填空题
设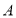 为非空实数集,若
为非空实数集,若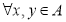 ,都有
,都有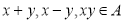 ,则称
,则称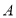 为封闭集.
为封闭集.
①集合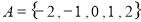 为封闭集;
为封闭集;
②集合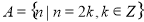 为封闭集;
为封闭集;
③若集合 为封闭集,则
为封闭集,则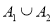 为封闭集;
为封闭集;
④若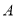 为封闭集,则一定有
为封闭集,则一定有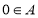 .
.
其中正确结论的序号是____________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省深圳市高三第一次调研考试文科数学试卷(解析版) 题型:选择题
已知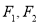 分别是双曲线
分别是双曲线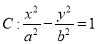 (
(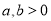 )的左、右焦点,点P在C上,若
)的左、右焦点,点P在C上,若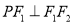 ,且
,且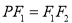 ,则C的离心率是( )
,则C的离心率是( )
A.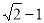 B.
B. C.
C. D.
D.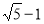
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com