
如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC.∠ABC=45°,AB=2 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.
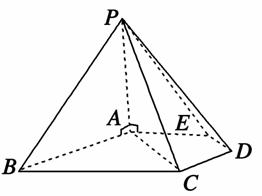
(1)求证:平面PCD⊥平面PAC;
(2)求直线PB与平面PCD所成角的大小;
(3)求四棱锥P-ACDE的体积.
[解析] (1)在△ABC中,因为∠ABC=45°,BC=4,
AB=2 ,
,
所以AC2=AB2+BC2-2AB·BC· cos45°=8,
因此AC=2 ,故BC2=AC2+AB2,
,故BC2=AC2+AB2,
所以∠BAC=90°.
又PA⊥平面ABCDE,AB∥CD,
所以CD⊥PA,CD⊥AC,
又PA,AC平面PAC,且PA∩AC=A,
所以CD⊥平面PAC.
又CD平面PCD,
所以平面PCD⊥平面PAC.
(2)由(1)知AB,AC,AP两两相互垂直,分别以AB、AC、AP为x轴、y轴、z轴建立如图所示的空间直角坐标系,由于△PAB是等腰三角形,所以PA=AB=2 .
.
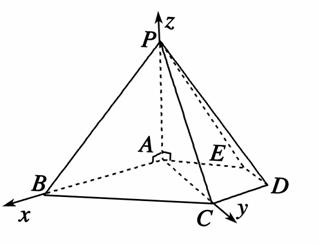
又AC=2 ,
,
因此A(0,0,0),B(2 ,0,0),C(0,2
,0,0),C(0,2 ,0),P(0,0,2
,0),P(0,0,2 ).
).
因为AC∥ED,CD⊥AC,
所以四边形ACDE是直角梯形.
因为AE=2,∠ABC=45°,AE∥BC,
所以∠BAE=135°,因此∠CAE=45°,
故CD=AE·sin45°=2×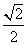 =
= ,
,
所以D(- ,2
,2 ,0).
,0).
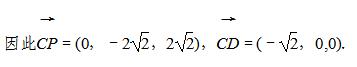
 因此直线PB与平面PCD所成的角为
因此直线PB与平面PCD所成的角为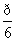 .
.
(3)因为AC∥ED,CD⊥AC,
所以四边形ACDE是直角梯形.
因为AE=2,∠ABC=45°,AE∥BC,
所以∠BAE=135°,因此∠CAE=45°,
故CD=AE·sin45°=2×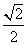 =
= ,
,
ED=AC-AE·cos45°=2 -2×
-2×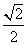 =
= ,
,
所以S四边形ACDE=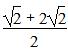 ×
× =3.
=3.
又PA⊥平面ABCDE,
所以VP-ACDE=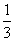 ×3×2
×3×2 =2
=2 .
.


科目:高中数学 来源: 题型:
对于四面体ABCD,给出下列四个命题:
①若AB=AC,BD=CD,则BC⊥AD;
②若AB=CD,AC=BD,则BC⊥AD;
③若AB⊥AC,BD⊥CD,则BC⊥AD;
④若AB⊥CD,AC⊥BD,则BC⊥AD.
其中真命题的序号是________.(把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
在平行六面体ABCD-A1B1C1D1中,向量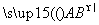 ,
,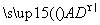 ,
,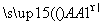 两两的夹角均为60°,且|
两两的夹角均为60°,且|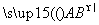 |=1,|
|=1,|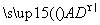 |=2,|
|=2,|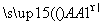 |=3,则|
|=3,则|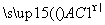 |=( )
|=( )
A.5 B.6
C.4 D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
根据下列条件,求圆的方程.
(1)圆心在原点且圆周被直线3x+4y+15=0分成12两部分的圆的方程;
(2)求经过两已知圆C1x2+y2-4x+2y=0与C2x2+y2-2y-4=0的交点,且圆心在直线l2x+4y=1上的圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com