
| θ |
| 2 |
| 1+sinθ |
| 1+sinθ+cosθ |
| 1 |
| 2 |
| π |
| 2 |
| 3 |
| 4 |
| 1-sin4θ |
| 1-sin4θ-cos4θ |
| θ |
| 2 |
| π |
| 2 |
2tan
| ||
1+tan2
|
1-tan2
| ||
1+tan2
|
(1+tan
| ||
1+tan2
|
| (1+t)2 |
| 1+t2 |
2(1+tan
| ||
1+tan2
|
| 2(1+t) |
| 1+t2 |
| 1+sinθ |
| 1+sinθ+cosθ |
| 1 |
| 2 |
| π |
| 2 |
| 3 |
| 4 |
| 1-sin4θ |
| 1-sin4θ-cos4θ |
| 1+sin(π+4θ) |
| 1+sin(π+4θ)+cos(π+4θ) |
| 1 |
| 2 |
| π |
| 2 |
| 7 |
| 8 |


科目:高中数学 来源: 题型:
| A、a5 |
| B、a6 |
| C、a10 |
| D、a11 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图是某电视剧在各年龄段人群收视情况的频率分布直方图.若某村观看此电视剧的观众人数为1400人,则其中50岁以上(含50岁)的观众约有( )人.
如图是某电视剧在各年龄段人群收视情况的频率分布直方图.若某村观看此电视剧的观众人数为1400人,则其中50岁以上(含50岁)的观众约有( )人.| A、504 | B、501 |
| C、500 | D、550 |
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高三上学期期中考试理科数学试卷(解析版) 题型:解答题
(本小题满分13分)在等比数列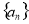 中,
中, 且
且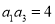 ,
, 是
是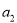 和
和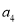 的等差中项.
的等差中项.
(Ⅰ)求数列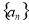 的通项公式;
的通项公式;
(Ⅱ)若数列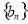 满足
满足 ,(
,( ),求数列
),求数列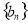 的前
的前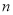 项和
项和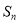 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com