Question

16．如图，在棱长为1的正方体ABCD-A₁B₁C₁D₁中，动点P在其表面上运动，且|PA|=x，把点的轨迹长度L=f（x）称为“喇叭花”函数，给出下列结论：
①$f（1）=\frac{3π}{4}$；②$f（\sqrt{2}）=\frac{3π}{2}$；③$f（\frac{{2\sqrt{3}}}{3}）=\frac{{5\sqrt{3}π}}{6}$；④$f（\frac{{\sqrt{21}}}{3}）=\frac{{\sqrt{3}π}}{3}$
其中正确的结论是：②③④．（填上你认为所有正确的结论序号）

Answer 1

分析 根据半径的长度，确定动点P的位置，在求出相应圆弧的半径及圆心角，即可求解．

解答 解：∵动点P在其表面上运动，且|PA|=x，
∴点的轨迹是以A为球心，PA为半径的球的球面与正方体的面的交线，
①当0＜x≤1时，点的轨迹如图（1），则f（x）=3×$\frac{1}{4}×2πx=\frac{3πx}{2}$，所以$f（1）=\frac{3π}{2}$，故①错；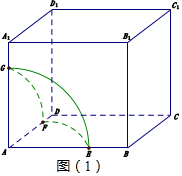
                                                
②当1$＜x＜\sqrt{2}$时，点P的轨迹在六个面都有，
x=$\frac{2\sqrt{3}}{3}$时，在与A相邻的三个面上的圆弧的圆心角为$\frac{π}{6}$，在另外三个面上都是四分之一圆弧，
∴$f（\frac{2\sqrt{3}}{3}）=3×\frac{1}{4}×2π×\frac{\sqrt{3}}{3}+\frac{1}{4}×2π×\frac{2\sqrt{3}}{3}$=$\frac{5\sqrt{3}π}{6}$，故③正确
③当x=$\sqrt{2}$时，如图（3）点P的轨迹是三段相等圆弧，圆弧的长是四分之一个圆，半径是1，
∴这条轨迹的长度是：3×$\frac{1}{4}×2π×1=\frac{3π}{2}$，故②正确；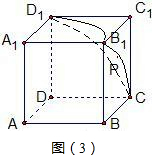

④当$\sqrt{2}＜x＜\sqrt{3}$时，点P的轨迹是三段相等圆弧，在与点A不相邻的三个面上，圆弧半径R=$\sqrt{（\frac{\sqrt{21}}{3}）^{2}-{1}^{2}}=\frac{2\sqrt{2}}{3}$，
圆弧的圆心角为$\frac{π}{6}$，∴f$（\frac{\sqrt{21}}{3}）=\frac{1}{4}×2π×\frac{2\sqrt{3}}{3}=\frac{\sqrt{3}}{3}π$，故④正确；
故答案为：②③④

点评 本题考查了空间轨迹问题，熟练掌握数形结合、分类讨论的思想方法、数形结合的思想方法是解题的关键．属于中档题，