
 已知抛物线C:y2=4x,点M与抛物线C的焦点F关于原点对称,过点M且斜率为k的直线l与抛物线C交于不同两点A,B,线段AB的中点为P,直线PF与抛物线C交于两点E,D.
已知抛物线C:y2=4x,点M与抛物线C的焦点F关于原点对称,过点M且斜率为k的直线l与抛物线C交于不同两点A,B,线段AB的中点为P,直线PF与抛物线C交于两点E,D.分析 (Ⅰ)设直线l的方程,代入抛物线方程,利用韦达定理及中点坐标公式求得P点坐标,求得直线PF的方程,代入抛物线方程,若四边形AEBD为平行四边形,当且仅当${x_1}+{x_2}=\frac{{4-2{k^2}}}{k^2}$=$\frac{{4{{(1-{k^2})}^2}}}{k^2}+2={x_3}+{x_4}$,即k2(k2-1)=0,求得k的值,由k不满足|k|<1且k≠0,故不存在k使得四边形AEBD为平行四边形.
(Ⅱ)由$\frac{{{{|{PF}|}^2}}}{{{{|{PM}|}^2}}}=\frac{{{{({\frac{2}{k^2}-2})}^2}+{{({\frac{2}{k}})}^2}}}{{{{({\frac{2}{k^2}})}^2}+{{({\frac{2}{k}})}^2}}}=\frac{{{k^4}-{k^2}+1}}{{{k^2}+1}}={k^2}+1+\frac{3}{{{k^2}+1}}-3$,根据k的取值范围,即可求得$\frac{{{{|{PF}|}^2}}}{{{{|{PM}|}^2}}}$的取值范围.
解答 解:(Ⅰ)设直线l的方程为y=k(x+1),
设A(x1,y1),B(x2,y2),E(x3,y3),D(x4,y4).
联立方程组$\left\{\begin{array}{l}y=k(x+1)\\{y^2}=4x\end{array}\right.$,整理得k2x2+(2k2-4)x+k2=0.
显然k≠0,且△>0,即(2k2-4)2-4k4>0,得|k|<1且k≠0.
得${x_1}+{x_2}=\frac{{4-2{k^2}}}{k^2}$,x1x2=1,…(4分)
${x_P}=\frac{{{x_1}+{x_2}}}{2}=\frac{2}{k^2}-1$,${y_P}=k[(\frac{2}{k^2}-1)+1]=\frac{2}{k}$.
直线PF的方程为:$y=\frac{k}{{1-{k^2}}}(x-1)$,
联立方程组$\left\{\begin{array}{l}y=\frac{k}{{1-{k^2}}}(x-1)\\{y^2}=4x\end{array}\right.$,
得$\frac{k^2}{{{{(1-{k^2})}^2}}}{x^2}+(\frac{{2{k^2}}}{{{{(1-{k^2})}^2}}}+4)x+\frac{k^2}{{{{(1-{k^2})}^2}}}=0$,
得${x_3}+{x_4}=\frac{{4{{(1-{k^2})}^2}}}{k^2}+2$,x3x4=1,…(6分)
若四边形AEBD为平行四边形,
当且仅当${x_1}+{x_2}=\frac{{4-2{k^2}}}{k^2}$=$\frac{{4{{(1-{k^2})}^2}}}{k^2}+2={x_3}+{x_4}$,
即k2(k2-1)=0,
得k=0,±1,与|k|<1且k≠0矛盾. …(8分)
故不存在实数k使得四边形AEBD为平行四边形; …(9分)
(Ⅱ)$\frac{{{{|{PF}|}^2}}}{{{{|{PM}|}^2}}}=\frac{{{{({\frac{2}{k^2}-2})}^2}+{{({\frac{2}{k}})}^2}}}{{{{({\frac{2}{k^2}})}^2}+{{({\frac{2}{k}})}^2}}}=\frac{{{k^4}-{k^2}+1}}{{{k^2}+1}}={k^2}+1+\frac{3}{{{k^2}+1}}-3$,…(11分)
由|k|<1且k≠0,得1<k2+1<2;
当${k^2}+1=\sqrt{3}$,$\frac{{{{|{PF}|}^2}}}{{{{|{PM}|}^2}}}$取得最小值$2\sqrt{3}-3$;
当k2+1=1时,$\frac{{{{|{PF}|}^2}}}{{{{|{PM}|}^2}}}$取1;当k2+1=2时,$\frac{{{{|{PF}|}^2}}}{{{{|{PM}|}^2}}}$取$\frac{1}{2}$;
所以$\frac{{{{|{PF}|}^2}}}{{{{|{PM}|}^2}}}∈[2\sqrt{3}-3,1)$.…(13分)
点评 本题考查抛物线的性质,直线与抛物线的位置关系,考查韦达定理,中点坐标公式,函数的最值与抛物线的应用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $2\sqrt{3}$ | C. | 6 | D. | $4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,动点P在其表面上运动,且|PA|=x,把点的轨迹长度L=f(x)称为“喇叭花”函数,给出下列结论:
如图,在棱长为1的正方体ABCD-A1B1C1D1中,动点P在其表面上运动,且|PA|=x,把点的轨迹长度L=f(x)称为“喇叭花”函数,给出下列结论:查看答案和解析>>
科目:高中数学 来源:2017届湖北省协作校高三联考一数学(文)试卷(解析版) 题型:解答题
已知函数 .
.
(1)若 ,求函数
,求函数 的极值和单调区间;
的极值和单调区间;
(2)若在区间 上至少存在一点
上至少存在一点 ,使得
,使得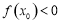 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com