
| A. | -1601 | B. | -1801 | C. | -2001 | D. | -2201 |
分析 设等差数列{an}的公差为d,由Sn=a1b1+a2b1q+${a}_{3}{b}_{1}{q}^{2}$+…+${a}_{n}{b}_{1}{q}^{n-1}$,(q≠1).利用“错位相减法”与等比数列的前n项和公式可得:
Sn=$\frac{{a}_{1}{b}_{1}-{a}_{n}{b}_{1}{q}^{n}}{1-q}$-db1$\frac{{q}^{n}-q}{(q-1)^{2}}$.不妨取m=2,可得S2=11,S4=7,S6=-201.化简可得:q2=4,b1(d+dq)=-6,b1(a1+a2q)=11.取q=-2,b1d=6,a1b1=-23.可得:S8=-201+${a}_{7}{b}_{1}{q}^{6}$+${a}_{8}{b}_{1}{q}^{7}$,代入化简即可得出.
解答 解:设等差数列{an}的公差为d,
由Sn=a1b1+a2b1q+${a}_{3}{b}_{1}{q}^{2}$+…+${a}_{n}{b}_{1}{q}^{n-1}$,(q≠1).
则qSn=a1b1q+${a}_{2}{b}_{1}{q}^{2}$+…+an-1${b}_{1}{q}^{n-1}$+${a}_{n}{b}_{1}{q}^{n}$,
∴(1-q)Sn=a1b1+db1(q+q2+…+qn-1)-${a}_{n}{b}_{1}{q}^{n}$=a1b1+db1$\frac{q({q}^{n-1}-1)}{q-1}$-${a}_{n}{b}_{1}{q}^{n}$,
∴Sn=$\frac{{a}_{1}{b}_{1}-{a}_{n}{b}_{1}{q}^{n}}{1-q}$-db1$\frac{{q}^{n}-q}{(q-1)^{2}}$,
不妨取m=2,
则S2=11,S4=7,S6=-201.
∴a1b1+a2b1q=11,a1b1+a2b1q+${a}_{3}{b}_{1}{q}^{2}$+${a}_{4}{b}_{1}{q}^{3}$=7,a1b1+a2b1q+${a}_{3}{b}_{1}{q}^{2}$+${a}_{4}{b}_{1}{q}^{3}$+${a}_{5}{b}_{1}{q}^{4}$+${a}_{6}{b}_{1}{q}^{5}$=-201,
可得q2=4,b1(d+dq)=-6,b1(a1+a2q)=11.
取q=-2,b1d=6,a1b1=-23.
S8=a1b1+a2b1q+${a}_{3}{b}_{1}{q}^{2}$+${a}_{4}{b}_{1}{q}^{3}$+${a}_{5}{b}_{1}{q}^{4}$+${a}_{6}{b}_{1}{q}^{5}$+${a}_{7}{b}_{1}{q}^{6}$+${a}_{8}{b}_{1}{q}^{7}$=-201+${a}_{7}{b}_{1}{q}^{6}$+${a}_{8}{b}_{1}{q}^{7}$=-201+(a1+6d)b1×64+(a1+7d)b1×(-128)
=-201+64(-a1b1-8db1)=-1801,
故选:B.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、“错位相减法”、取特殊值方法,考查了推理能力与计算能力,属于难题.


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -2 | C. | 1 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于直线x=$\frac{π}{6}$对称 | B. | 关于直线x=-$\frac{π}{12}$对称 | ||
| C. | 关于点($\frac{2π}{3}$,0)对称 | D. | 关于点(π,0)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 车流量x(万辆) | 100 | 102 | 108 | 114 | 116 |
| PM2.5的浓度y(微克/立方米) | 78 | 80 | 84 | 88 | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
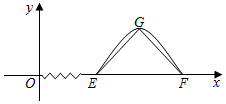 已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是以G为顶点,EF为底边且长为4的等腰直角三角形,则f(100)=( )
已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是以G为顶点,EF为底边且长为4的等腰直角三角形,则f(100)=( )| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com