
【题目】如图 1,在直角梯形![]() 中,
中, ![]() ,且
,且![]() .现以
.现以![]() 为一边向外作正方形
为一边向外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使
翻折,使![]() 平面与平面
平面与平面![]() 垂直,
垂直, ![]() 为
为![]() 的中点,如图 2.
的中点,如图 2.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析:
(1)取EC中点N,连结MN,BN.由几何关系可证得四边形ABNM为平行四边形.则BN∥AM,利用线面平行的判定定理可得![]() 平面
平面![]() ;
;
(2) 由几何关系有ED⊥AD,利用面面垂直的性质定理可得ED⊥平面ABCD,则ED⊥BC,利用直角梯形的性质结合勾股定理可得BC⊥BD,据此由线面垂直的判定定理有![]() 平面
平面![]() ;
;
(3) 作![]() 平面PEC于点H,连接CH,则∠DCH为所求的角,利用三棱锥体积相等转化顶点有:
平面PEC于点H,连接CH,则∠DCH为所求的角,利用三棱锥体积相等转化顶点有: ![]() ,据此可求得
,据此可求得![]() ,利用三角函数的定义可得
,利用三角函数的定义可得![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]() .
.
试题解析:
(1)证明:取![]() 中点
中点![]() ,连结
,连结![]() .
.
在![]() 中,
中, ![]() 分别为
分别为![]() 的中点,
的中点,
所以![]() ,且
,且![]() .
.
由已知![]() ,
,
所以四边形![]() 为平行四边形.
为平行四边形.
所以![]() .
.
又因为![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)证明:在正方形![]() 中,
中, ![]() ,
,
又因为平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
所以![]()
在直角梯形![]() 中,
中, ![]() ,可得
,可得![]() .
.
在![]() 中,
中, ![]() .
.
所以![]() .
.
所以![]() 平面
平面![]() .
.
(3)作![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() 为所求的角
为所求的角
由(2)知, ![]()
所以![]() ,又因为
,又因为![]() 平面
平面![]()
又![]() .
.
所以, ![]()
 .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面为正方形
中,底面为正方形![]() ,
, ![]() 底面
底面![]() ,该四棱锥的正视图和侧视图均为腰长为6的等腰直角三角形.
,该四棱锥的正视图和侧视图均为腰长为6的等腰直角三角形.

(1)画出相应的俯视图,并求出该俯视图的面积;
(2)求证: ![]() ;
;
(3)求四棱锥![]() 外接球的直径.
外接球的直径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:关于x的不等式x2+(a﹣1)x+a2≤0的解集为;命题q:函数f(x)=(4a2+7a﹣1)x是增函数,若¬p∧q为真,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
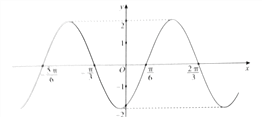
【题目】函数![]() 的图象如图所示,为了得到函数
的图象如图所示,为了得到函数![]() 的图象,可以把函数
的图象,可以把函数![]() 的图象( )
的图象( )
A. 每个点的横坐标缩短到原来的![]() (纵坐标不变),再向左平移
(纵坐标不变),再向左平移![]() 个单位
个单位
B. 每个点的横坐标缩短到原来的2倍(纵坐标不变),再向左平移![]() 个单位
个单位
C. 先向左平移![]() 个单位,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变)
个单位,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变)
D. 先向左平移![]() 个单位,再把所得各点的横坐标伸长到原来的
个单位,再把所得各点的横坐标伸长到原来的![]() (纵坐标不变)
(纵坐标不变)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设[x]表示不超过x的最大整数,如:[π]=3,[﹣4.3]=﹣5.给出下列命题: ①对任意实数x,都有[x]﹣x≤0;
②若x1≤x2 , 则[x1]≤[x2];
③[lg1]+[lg2]+[lg3]+…+[lg100]=90;
④若函数f(x)= ![]() ﹣
﹣ ![]() ,则y=[f(x)]+[f(﹣x)]的值域为{﹣1,0}.
,则y=[f(x)]+[f(﹣x)]的值域为{﹣1,0}.
其中所有真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知线段![]() 的端点
的端点![]() ,端点
,端点![]() 在圆
在圆![]() 上运动
上运动
(Ⅰ)求线段![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
(Ⅱ) 设动直线![]() 与圆
与圆![]() 交于
交于![]() 两点,问在
两点,问在![]() 轴正半轴上是否存在定点
轴正半轴上是否存在定点![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称?若存在,请求出点
轴对称?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为 ![]() 的正方形,AA1=3,E是AA1的中点,过C1作C1F⊥平面BDE与平面ABB1A1交于点F,则
的正方形,AA1=3,E是AA1的中点,过C1作C1F⊥平面BDE与平面ABB1A1交于点F,则 ![]() =
=
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文科)设函数f(x)=x2﹣2ax﹣8a2(a>0),记不等式f(x)≤0的解集为A.
(1)当a=1时,求集合A;
(2)若(﹣1,1)A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() ,且满足
,且满足![]() .
.
(1)判断函数![]() 在
在![]() 上的单调性,并用定义证明;
上的单调性,并用定义证明;
(2)设函数![]() ,求
,求![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(3)若存在实数m,使得关于x的方程![]() 恰有4个不同的正根,求实数m的取值范围.
恰有4个不同的正根,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com