
 如图所示,一艘海轮从A处出发,测得灯塔在海轮的北偏东15°方向,与海轮相距20海里的B处,海轮按北偏西60°的方向航行了30分钟后到达C处,又测得灯塔在海轮的北偏东75°的方向,则海轮的速度为$\frac{2}{3}$($\sqrt{3}$-1)海里/分钟.
如图所示,一艘海轮从A处出发,测得灯塔在海轮的北偏东15°方向,与海轮相距20海里的B处,海轮按北偏西60°的方向航行了30分钟后到达C处,又测得灯塔在海轮的北偏东75°的方向,则海轮的速度为$\frac{2}{3}$($\sqrt{3}$-1)海里/分钟. 分析 分别求得∠A和∠B,∠C,利用正弦定理求得AC,最后除以时间.
解答  解:根据题意知∠BAC=60°,∠C=45°,∠ABC=105°
解:根据题意知∠BAC=60°,∠C=45°,∠ABC=105°
∴sin∠CBA=sin45°cos60°+cos45°sin60°=$\frac{\sqrt{2}+\sqrt{6}}{4}$.
∴由正弦定理知AC=$\frac{AB}{sinB}$•sinC=$\frac{20}{\frac{\sqrt{2}+\sqrt{6}}{4}}$×$\frac{\sqrt{2}}{2}$=20($\sqrt{3}$-1).
V=$\frac{AC}{30}$=$\frac{2}{3}$($\sqrt{3}$-1)(海里/分钟).
即海轮的速度为$\frac{2}{3}$($\sqrt{3}$-1)海里/分钟.
故答案为:$\frac{2}{3}$($\sqrt{3}$-1).
点评 本题主要考查了正弦定理在解三角形中的应用.考查了学生分析问题和解决实际问题的能力.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
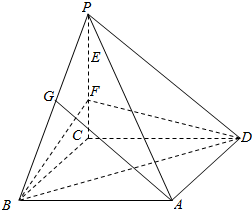 如图,在四棱锥P-ABCD中,已知底面ABCD是平行四边形,E、F是PC的三等分点,G是PB的中点,过E,A,G三点的平面?FBD是否平行?
如图,在四棱锥P-ABCD中,已知底面ABCD是平行四边形,E、F是PC的三等分点,G是PB的中点,过E,A,G三点的平面?FBD是否平行?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com