
分析 由题意可知,数列{an}是首项为a1,公差为$\frac{d}{2}$的等差数列,代入方差公式即可求得d.
解答 解:由2an=2an-1+d(n≥2),得an-an-1=$\frac{d}{2}$(n≥2),
∴数列{an}是首项为a1,公差为$\frac{d}{2}$的等差数列,
数据a1,a2,a3,a4,a5,a6,a7的平均数为a4,
∴$\frac{1}{7}[({a}_{1}-{a}_{4})^{2}+…+({a}_{7}-{a}_{4})^{2}]=9$,
即$\frac{1}{7}[(3×\frac{d}{2})^{2}+(2×\frac{d}{2})^{2}+…+(3×\frac{d}{2})^{2}]=9$,
∴$\frac{9}{4}{d}^{2}+{d}^{2}+\frac{{d}^{2}}{4}+0+\frac{{d}^{2}}{4}+{d}^{2}+\frac{9}{4}{d}^{2}$=63,
即d2=9,d=±3.
故答案为:±3.
点评 本题考查等差数列的通项公式,考查一组数据的方差,是基础的计算题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
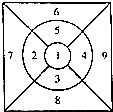 如图,图案共分9个区域,有6种不同颜色的涂料可供涂色,每个区域只能涂一种颜色的涂料,其中2和9同色、3和6同色、4和7同色、5和8同色,且相邻区域的颜色不相同,则涂色方法有( )
如图,图案共分9个区域,有6种不同颜色的涂料可供涂色,每个区域只能涂一种颜色的涂料,其中2和9同色、3和6同色、4和7同色、5和8同色,且相邻区域的颜色不相同,则涂色方法有( )| A. | 360种 | B. | 720种 | C. | 780种 | D. | 840种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com