
分析 ( 1)设椭圆的半焦距为c,由已知得$2a+2c=4+2\sqrt{3}$,又$\frac{c}{a}=\frac{{\sqrt{3}}}{2}$,a2=b2+c2,联立解出即可得出.
(2)由题意可知,直线l的斜率存在且不为0,故可设直线l的方程为y=kx+m(m≠0),P(x1,y1),Q(x2,y2),与椭圆方程联立消去y得(1+4k2)x2+8kmx+4(m2-1)=0,△>0,即4k2-m2+1>0.由直线OP,PQ,OQ的斜率依次成等比数列,可得$\frac{{y}_{1}}{{x}_{1}}$•$\frac{{y}_{2}}{{x}_{2}}$=k2.解得k.利用弦长公式与三角形面积计算公式即可得出.
解答 解:( 1)设椭圆的半焦距为c,由已知得$2a+2c=4+2\sqrt{3}$,
又$\frac{c}{a}=\frac{{\sqrt{3}}}{2}$,a2=b2+c2,
解得$a=2,c=\sqrt{3},b=1$,
∴椭圆C的标准方程为$\frac{x^2}{4}+{y^2}=1$.
(2)由题意可知,直线l的斜率存在且不为0,
故可设直线l的方程为y=kx+m(m≠0),P(x1,y1),Q(x2,y2),
由$\left\{\begin{array}{l}y=kx+m\\{x^2}+4{y^2}-4=0\end{array}\right.$,消去y得(1+4k2)x2+8kmx+4(m2-1)=0,
则△=64k2m2-16(1+4k2)(m2-1)=16(4k2-m2+1)>0,即4k2-m2+1>0,
且${x_1}+{x_2}=-\frac{8km}{{1+4{k^2}}}$,${x_1}{x_2}=\frac{{4({m^2}-1)}}{{1+4{k^2}}}$,
故${y_1}{y_2}=(k{x_1}+m)(k{x_2}+m)={k^2}{x_1}{x_2}+km({x_1}+{x_2})+{m^2}$.
∵直线OP,PQ,OQ的斜率依次成等比数列,
∴$\frac{y_1}{x_1}•\frac{y_2}{x_2}=\frac{{{k^2}{x_1}{x_2}+km({x_1}+{x_2})+{m^2}}}{{{x_1}{x_2}}}={k^2}$.
即$\frac{{-8{k^2}{m^2}}}{{1+4{k^2}}}+{m^2}=0$,又m≠0,∴${k^2}=\frac{1}{4}$,即$k=±\frac{1}{2}$,
又∵4k2-m2+1>0,∴0<m2<2,由于直线OP,OQ的斜率存在,∴m2≠1.
故${S_{△OPQ}}=\frac{1}{2}|{{x_1}-{x_2}}|•|m|=\frac{1}{2}\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}|m|=\frac{1}{2}\sqrt{{{(\frac{-8km}{{1+4{k^2}}})}^2}-4×\frac{{4({m^2}-1)}}{{1+4{k^2}}}}•|m|$=$\sqrt{{m^2}(2-{m^2})}$.
令t=m2,则0<t<2,且t≠1,记f(t)=t(2-t)=-t2+2t,
∴f(t)的值域为(0,1).
故△OPQ面积的取值范围为(0,1).
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、一元二次方程的根与系数的关系、三角形面积计算公式、斜率计算公式、等比数列的性质、函数的单调性,考查了推理能力与计算能力,属于难题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{7}$ | B. | $\frac{5}{3}$ | C. | $\frac{11}{7}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2<x<1} | B. | {x|-2<x<2} | C. | {x|2≤x<3} | D. | {x|x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
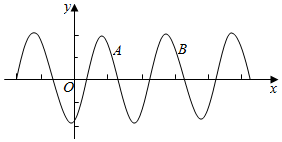 已知函数f(x)=2cos(ωx-φ)(ω>0,φ∈[0,π]的部分图象如图所示,若A($\frac{π}{2}$,$\sqrt{2}$),B($\frac{3π}{2}$,$\sqrt{2}$),则函数f(x)的单调增区间为( )
已知函数f(x)=2cos(ωx-φ)(ω>0,φ∈[0,π]的部分图象如图所示,若A($\frac{π}{2}$,$\sqrt{2}$),B($\frac{3π}{2}$,$\sqrt{2}$),则函数f(x)的单调增区间为( )| A. | [-$\frac{π}{4}$+2kπ,$\frac{3π}{4}$+2kπ](k∈Z) | B. | [$\frac{3π}{4}$+2kπ,$\frac{7π}{4}$+2kπ](k∈Z) | ||
| C. | [-$\frac{π}{8}$+kπ,$\frac{3π}{8}$+kπ](k∈Z) | D. | [$\frac{3π}{8}$+kπ,$\frac{7π}{8}$+kπ](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com