
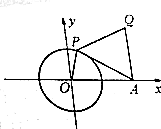
 已知A(2,0),点P在以原点O为圆心、半径为1的圆周上运动.以PA为边向外作正三角形APQ,多边形OPQA的面积为S.
已知A(2,0),点P在以原点O为圆心、半径为1的圆周上运动.以PA为边向外作正三角形APQ,多边形OPQA的面积为S.分析 (1)f(θ)=SPOAQ=S△POA+S△PQA.设∠AOP=θ.即可求S=f(θ)的表达式;
(2)设点P的横坐标为x,x=cosθ,y=sinθ,即可求S=g(x)的表达式;
(3)请选择(1)中的一种方法,利用三角函数知识求S的最大值.
解答 解:(1)f(θ)=SPOAQ=S△POA+S△PQA.
S△POA=$\frac{1}{2}$OPsinθ×OA=sinθ[由对称性只考虑上半平面∴θ∈(0,π)]
S△PQA=$\frac{1}{2}$PQ×PAsin$\frac{π}{3}$=$\frac{\sqrt{3}}{4}$PA2=$\frac{\sqrt{3}}{4}$(PO2+OA2-2PO×OA)
=$\frac{\sqrt{3}}{4}$(5-4cosθ)
∴f(θ)=sinθ+$\frac{\sqrt{3}}{4}$(5-4cosθ)=$\frac{5\sqrt{3}}{4}$+sinθ-$\sqrt{3}$cosθ;
(2 )设P(x,y)在单位圆中,x=cosθ,y=sinθ,
由对称性只考虑上半平面 x∈(-1,1)]
g(x)=$\frac{5\sqrt{3}}{4}$+y-$\sqrt{3}$x=$\frac{5\sqrt{3}}{4}$+$\sqrt{1-{x}^{2}}$-$\sqrt{3}$x;
(3)f(θ)=$\frac{5\sqrt{3}}{4}$+sinθ-$\sqrt{3}$cosθ=$\frac{5\sqrt{3}}{4}$+2sin(θ-$\frac{π}{3}$)
∴sin(θ-$\frac{π}{3}$)=1,f(θ)max=$\frac{5\sqrt{3}}{4}$+2.
点评 本题考查利用数学知识解决实际问题,考查四边形面积的计算,考查学生分析解决问题的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 给定椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),称圆心在原点O,半径为$\sqrt{{a}^{2}+{b}^{2}}$的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F($\sqrt{2}$,0),其短轴上的一个端点到F的距离为$\sqrt{3}$.
给定椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),称圆心在原点O,半径为$\sqrt{{a}^{2}+{b}^{2}}$的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F($\sqrt{2}$,0),其短轴上的一个端点到F的距离为$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}-1}}{2}-\frac{{\sqrt{2}+1}}{2}i$ | B. | $\frac{{\sqrt{2}+1}}{2}-\frac{{\sqrt{2}-1}}{2}i$ | C. | $\frac{1}{2}+\frac{3}{2}i$ | D. | $\frac{1}{2}-\frac{3}{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | $\sqrt{13}$ | C. | 17 | D. | $\sqrt{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
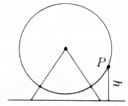 如图是某游乐场的摩天轮的示意图,其最高点离地面45米,直径为40米,并以每12分钟一周的速度匀速旋转,求证:摩天轮上某个点P离地面的高度h(米)与时间t(分)的函数关系式是h=-20cos$\frac{π}{6}$t+25.
如图是某游乐场的摩天轮的示意图,其最高点离地面45米,直径为40米,并以每12分钟一周的速度匀速旋转,求证:摩天轮上某个点P离地面的高度h(米)与时间t(分)的函数关系式是h=-20cos$\frac{π}{6}$t+25.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{e_1},\overrightarrow{e_1}-\overrightarrow{e_2}$ | B. | $\overrightarrow{e_1}+\overrightarrow{e_2},\overrightarrow{e_1}-\overrightarrow{e_2}$ | ||
| C. | $\overrightarrow{e_1}+2\overrightarrow{e_2},-2\overrightarrow{e_1}+\overrightarrow{e_2}$ | D. | $\overrightarrow{e_1}-\overrightarrow{3{e_2}},-2\overrightarrow{e_1}+6\overrightarrow{e_2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com