
 ������ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������Բ����ԭ��O���뾶Ϊ$\sqrt{{a}^{2}+{b}^{2}}$��Բ����ԲC�ġ�Բ��������ԲC��һ������ΪF��$\sqrt{2}$��0����������ϵ�һ���˵㵽F�ľ���Ϊ$\sqrt{3}$��
������ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������Բ����ԭ��O���뾶Ϊ$\sqrt{{a}^{2}+{b}^{2}}$��Բ����ԲC�ġ�Բ��������ԲC��һ������ΪF��$\sqrt{2}$��0����������ϵ�һ���˵㵽F�ľ���Ϊ$\sqrt{3}$������ ��1��������Բ�Ķ����뼸�����ʣ����a��b��ֵ������д����Բ�ķ��̺�Բ���̣�
��2��������д������P������Բ���е�ֱ�ߣ�����Բ������ɷ����飬����������ֻ��һ��⣬
�ɴ�������ߵķ��̣���֤����ֱ�ߴ�ֱ��
������������ֱ��l1��l2����һ��б�ʲ�����ʱ������l1��l2��ֱ��
��l1��l2б�ʴ���ʱ���ó�l1��l2��ֱ����l1��l2������P���ֱ���Բ�ڵ�M��N���Ӷ��ó��߶�MN�ij�ΪԲ��ֱ�����Ƕ�ֵ��
��� �⣺��1����c=$\sqrt{2}$��a=$\sqrt{3}$����b=$\sqrt{{a}^{2}{-c}^{2}}$=1��
����Բ����Ϊ$\frac{{x}^{2}}{3}$+y2=1��Բ����Ϊx2+y2=4��
��2����������ΪԲx2+y2=4��y��������Ľ���ΪP��0��2����
�����P��0��2��������Բ���е�ֱ��Ϊy=kx+2��
������$\left\{\begin{array}{l}{y=kx+2}\\{\frac{{x}^{2}}{3}{+y}^{2}=1}\end{array}\right.$�ã�1+3k2��x2+12kx+9=0��
��Ϊֱ��y=kx+2����Բ���У����ԡ�=144k2-4��9��1+3k2��=0�����k=��1��
����ֱ��l1��l2�ķ���Ϊy=x+2��y=-x+2��
��k1•k2=-1����l1��l2��
�������ٵ�ֱ��l1��l2����һ��б�ʲ�����ʱ��������ֱ��l1б�ʲ����ڣ�
��l1��x=��$\sqrt{3}$����l1��x=$\sqrt{3}$ʱ��l1��Բ���ڵ㣨$\sqrt{3}$��1���ͣ�$\sqrt{3}$��-1����
��ʱl2Ϊy=1����y=-1������Ȼֱ��l1��l2��ֱ��
ͬ����֤��l1��x=-$\sqrt{3}$ʱ��ֱ��l1��l2��ֱ��
�ڵ�l1��l2б�ʴ���ʱ�����P��x0��y0��������${{x}_{0}}^{2}$+${{y}_{0}}^{2}$=4��
�辭����P��x0��y0������Բ���е�ֱ��Ϊy=t��x-x0��+y0��
������$\left\{\begin{array}{l}{y=t��x{-x}_{0}��{+y}_{0}}\\{\frac{{x}^{2}}{3}{+y}^{2}=1}\end{array}\right.$��
�ã�1+3t2��x2+6t��y0-tx0��x+3${{��y}_{0}-{tx}_{0}��}^{2}$-3=0��
�ɡ�=0���������ã�3-${{x}_{0}}^{2}$��t2+2x0y0t+1-${{y}_{0}}^{2}$=0��
��Ϊ${{x}_{0}}^{2}$+${{y}_{0}}^{2}$=4�������У�3-${{x}_{0}}^{2}$��t2+2x0y0t+��${{x}_{0}}^{2}$-3��=0��
��l1��l2��б�ʷֱ�Ϊt1��t2����Ϊl1��l2����Բ���У�
����t1��t2�����������̣�3-${{x}_{0}}^{2}$��t2+2x0y0t+��${{x}_{0}}^{2}$-3��=0��
����t1•t2=-1����l1��l2��ֱ��
�ۺϢ٢�֪����Ϊl1��l2������P��x0��y0����
�ֱַ���Բ�ڵ�M��N����l1��l2 ��ֱ��
�����߶�MNΪԲx2+y2=4��ֱ����|MN|=4��
�����߶�MN�ij�Ϊ��ֵ��
���� ���⿼������Բ�Ķ����뼸�����ʵ�Ӧ�����⣬Ҳ�������¶����Ӧ�����⣬������ֱ����Բ���ߵ�Ӧ�������Լ���������˼���Ӧ�����⣬���ۺ�����Ŀ��


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
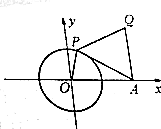 ��֪A��2��0������P����ԭ��OΪԲ�ġ��뾶Ϊ1��Բ�����˶�����PAΪ����������������APQ�������OPQA�����ΪS��
��֪A��2��0������P����ԭ��OΪԲ�ġ��뾶Ϊ1��Բ�����˶�����PAΪ����������������APQ�������OPQA�����ΪS���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com