练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．若（x+$\frac{1}{2x}$）n的展开式中前3项的系数成等差数列，则其展开式中所有项的二项式系数之和是（　　）
    A．28B．27C．1D．0

    分析 利用二项式展开式的通项公式求出展开式中前3项的系数，再根据它们成等差数列求得n的值，可得展开式中所有项的二项式系数之和为2n的值．

    解答 解：∵（x+$\frac{1}{2x}$）n的展开式中前3项的系数分别为1，$\frac{1}{2}$n，${C}_{n}^{2}$•${（\frac{1}{2}）}^{2}$，
    根据它们成等差数列，可得1+${C}_{n}^{2}$•${（\frac{1}{2}）}^{2}$=n，∴n=8，
    则其展开式中所有项的二项式系数之和为2n=28，
    故选：A．

    点评 本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

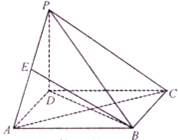    7．如图，四棱锥P-ABCD的底面ABCD是正方形，PD⊥底面ABCD，PD=AB，
    （1）若E为PA的中点，求异面直线AC与BE所成角的余弦值；
    （2）若点F在侧棱PC上，二面角F-BD-C的余弦值为$\frac{\sqrt{3}}{3}$，求$\frac{PF}{PC}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知函数f（x）=x2+mx+n，且y=f（x+2）的图象关于y轴对称，则大小关系正确的是（　　）
    A．f（$\frac{5}{2}$）＜f（1）＜f（$\frac{7}{2}$）B．f（1）＜f（$\frac{7}{2}$）＜f（$\frac{5}{2}$）C．f（$\frac{7}{2}$）＜f（1）＜f（$\frac{5}{2}$）D．f（$\frac{7}{2}$）＜f（$\frac{5}{2}$）＜f（1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知$\overrightarrow a，\;\overrightarrow b$为同向单位向量，若$\overrightarrow a•\overrightarrow b=\frac{{1+4{k^2}}}{4k}$（k＞0），则k=$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

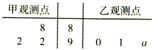    12．如图，茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数（AQI）．乙观测点记录中有一个数字模糊无法确认，已知该数是0，1，…，9中随机的一个数，并在图中以a表示．
    （Ⅰ）求乙观测点记录的AQI的平均值超过甲观测点记录的AQI的平均值的概率；
    （Ⅱ）当a=2时，分别从甲、乙两观测点记录的数据中各随机抽取一天的观测值，记这两观测值之差的绝对值为X，求随机变量X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．某用水量较大的企业为积极响应政府号召的“节约用水，我们共同的责任”的倡议，对生产设备进行技术改造，下表提供了该企业节约用水技术改造后生产甲产品过程中记录的产量x（吨）与相应的生产用水y（吨）的几组对照数据：
    x1234
    y0.40.91.11.6
    （1）若x，y之间是线性相关，请根据表中提供的数据，求y关于x的线性回归方程y=bx+a；
    （2）已知该厂技术改造前100吨甲产品的生产用水为120吨，试根据（1）中求出的线性回归方程，预测技术改造后生产100吨甲产品的用水量比技术改造前减少了多少吨？
    （参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{1}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n\stackrel{-2}{x}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．等比数列{an}的各项均为正数，且a2=4，a42=4a1a5．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）设bn=log2a1+log2a2+log2a3+…+log2an，求数列{$\frac{1}{{b}_{n}}$}的前n项和Sn，并证明：Sn＜2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ，$\overrightarrow{a}=（1，1）$，$\overrightarrow{a}+3\overrightarrow{b}=（4，-2）$，则cosθ=（　　）
    A．0B．$\frac{3}{5}$C．$\frac{\sqrt{2}}{2}$D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．设椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点分别为F1，F2，过右焦点F2的直线l与C相交于P，Q两点，若△F1PQ的周长为短轴长的2$\sqrt{2}$倍，抛物线y2=2$\sqrt{2}$x的焦点F满足$\overrightarrow{{F}_{1}F}$=3$\overrightarrow{F{F}_{2}}$．
    （I） 求椭圆C的方程；
    （Ⅱ）若$\overrightarrow{P{F}_{2}}$=3$\overrightarrow{{F}_{2}Q}$，求直线l的方程；
    （Ⅲ）若直线l的倾斜角α∈[$\frac{π}{6}$，$\frac{π}{2}$]，求△F1PQ的内切圆的半径r的取值范围．

    查看答案和解析>>

    同步练习册答案