考点:平面与平面平行的判定,点、线、面间的距离计算
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明面CEI∥平面A1BD,只需证明EI∥平面A1BD,CE∥平面A1BD,利用三角形的中位线、平行四边形的性质可以证明;
(3)先说明连接EH,则∠EHC为CH与平面AA1B所成的角,再在△CEH中,利用正切函数,即可得到结论.
解答:
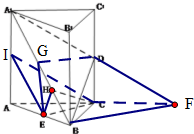
解:(1)∵E,I分别是AB,AA
1的中点,
∴EI∥BA
1,
∵EI?平面A
1BD,BA
1?平面A
1BD,
∴EI∥平面A
1BD,
取BA
1的中点G,连接EG,DG,
∴GE平行且等于
AA
1,
∵D是CC
1中点,
∴CD平行且等于
AA
1,
∴GE平行且等于CD,
∴四边形GDCE是平行四边形,
∴CE∥GD,
∵CE?平面A
1BD,GD?平面A
1BD,
∴CE∥平面A
1BD,
∵CE∩EI=E,
∴平面A
1BD∥面CEI;
(2)∵AA
1⊥面ABC,CE?面ABC,
∴AA
1⊥CE
又△ABC等边三角形,E是中点,
∴
CE⊥AB,CE=AB=所以CE⊥面AA
1B,
连接EH,则∠EHC为CH与平面AA
1B所成的角,
在Rt△CEH中,tan∠EHC==,
所以EH最短时∠EHC最大
此时,EH⊥A
1B,
∴
tan∠EHC===,∴
EH=由平几相似关系得AA
1=4.
点评:本题考查线面垂直,线面平行,考查线面角,解题的关键是掌握面面平行的判定方法,正确作出线面角.

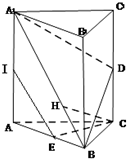 如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E,I分别是CC1,AB,AA1的中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E,I分别是CC1,AB,AA1的中点. 解:(1)∵E,I分别是AB,AA1的中点,
解:(1)∵E,I分别是AB,AA1的中点,
