
已知函数f(x)=sin (2x+φ),其中φ为实数,若f(x)≤ 对x∈R恒成立,且
对x∈R恒成立,且 <f(π),则下列结论正确的是( ).
<f(π),则下列结论正确的是( ).
A. =-1
=-1
B.f >f
>f
C.f(x)是奇函数
D.f(x)的单调递增区间是 (k∈Z)
(k∈Z)
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(解析版) 题型:解答题
已知函数f(x)= 的图象过原点,且关于点(-1,2)成中心对称.
的图象过原点,且关于点(-1,2)成中心对称.
(1)求函数f(x)的解析式;
(2)若数列{an}满足a1=2,an+1=f(an),试证明数列 为等比数列,并求出数列{an}的通项公式.
为等比数列,并求出数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(解析版) 题型:选择题
已知随机变量X~N(1,4)且P(X<2)=0.72,则P(1<X<2)等于( ).
A.0.36 B.0.16 C.0.22 D.0.28
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练x4-1练习卷(解析版) 题型:填空题
如图,点A、B、C都在⊙O上,过点C的切线交AB的延长线于点D,若AB=5,BC=3,CD=6,则线段AC的长为________.
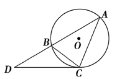
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(解析版) 题型:解答题
已知函数f(x)=2sin ωx·cos ωx+2 cos2ωx-
cos2ωx- (其中ω>0),且函数f(x)的周期为π.
(其中ω>0),且函数f(x)的周期为π.
(1)求ω的值;
(2)将函数y=f(x)的图象向右平移 个单位长度,再将所得图象各点的横坐标缩小到原来的
个单位长度,再将所得图象各点的横坐标缩小到原来的 倍(纵坐标不变)得到函数y=g(x)的图象,求函数g(x)在
倍(纵坐标不变)得到函数y=g(x)的图象,求函数g(x)在 上的单调区间.
上的单调区间.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(解析版) 题型:解答题
已知函数f(x)=ex-ln(x+m).
(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(2)当m≤2时,证明f(x)>0.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(解析版) 题型:选择题
已知f(x)是定义在(0,+∞) 上的非负可导函数,且满足xf′(x)+f(x)≤0,对任意的0<a<b,则必有( ).
A.af(b)≤bf(a) B.bf(a)≤af(b)
C.af(a)≤f(b) D.bf(b)≤f(a)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练3练习卷(解析版) 题型:解答题
已知函数f(x)=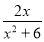 .
.
(1)若f(x)>k的解集为{x|x<-3,或x>-2},求k的值;
(2)对任意x>0,f(x)≤t恒成立,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习6-2椭圆、双曲线、抛物线练习卷(解析版) 题型:解答题
已知椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4
,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4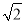 .
.
(1)求椭圆C的方程;
(2)若过点M(2,0)的直线与椭圆C相交于两点A、B,设P为椭圆上一点,且满足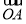 +
+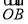 =t
=t (O为坐标原点),当|
(O为坐标原点),当|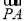 -
-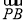 |<
|<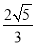 时,求实数t的取值范围.
时,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com