
已知椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4
,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4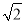 .
.
(1)求椭圆C的方程;
(2)若过点M(2,0)的直线与椭圆C相交于两点A、B,设P为椭圆上一点,且满足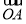 +
+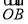 =t
=t (O为坐标原点),当|
(O为坐标原点),当|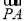 -
-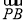 |<
|<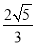 时,求实数t的取值范围.
时,求实数t的取值范围.
(1)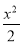 +y2=1.(2)
+y2=1.(2)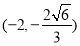 ∪
∪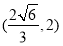
【解析】(1)由题意知椭圆的离心率e=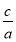 =
=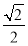 ,∴e2=
,∴e2=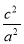 =
=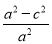 =
=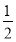 ,
,
即a2=2b2.
又△EGF2的周长为4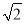 ,即4a=4
,即4a=4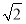 ,∴a2=2,b2=1.
,∴a2=2,b2=1.
∴椭圆C的方程为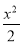 +y2=1.
+y2=1.
(2)由题意知直线AB的斜率存在,即t≠0.
设直线AB的方程为y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),由 ,
,
得(1+2k2)x2-8k2x+8k2-2=0.
由Δ=64k4-4(2k2+1)(8k2-2)>0,得k2<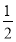 .x1+x2=
.x1+x2=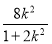 ,x1x2=
,x1x2=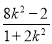 ,
,
∵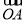 +
+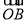 =t
=t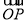 ,
,
∴(x1+x2,y1+y2)=t(x,y),x=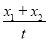 =
=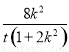 ,y=
,y=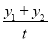 =
=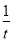 [k(x1+x2)-4k]=
[k(x1+x2)-4k]=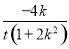 .
.
∵点P在椭圆C上,
∴ +2
+2 =2,
=2,
∴16k2=t2(1+2k2).
∵|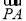 -
-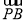 |<
|<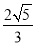 ,∴
,∴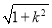 |x1-x2|<
|x1-x2|<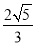 ,
,
∴(1+k2)[(x1+x2)2-4x1x2]<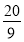 ,
,
∴(1+k2)  <
<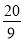 ,
,
∴(4k2-1)(14k2+13)>0,
∴k2>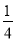 .∴
.∴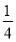 <k2<
<k2<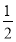 .
.
∵16k2=t2(1+2k2),∴t2=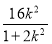 =8-
=8-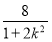 ,
,
又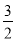 <1+2k2<2,∴
<1+2k2<2,∴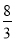 <t2=8-
<t2=8-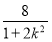 <4,
<4,
∴-2<t<- 或
或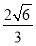 <t<2,
<t<2,
∴实数t的取值范围为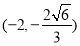 ∪
∪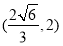


科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(解析版) 题型:选择题
已知函数f(x)=sin (2x+φ),其中φ为实数,若f(x)≤ 对x∈R恒成立,且
对x∈R恒成立,且 <f(π),则下列结论正确的是( ).
<f(π),则下列结论正确的是( ).
A. =-1
=-1
B.f >f
>f
C.f(x)是奇函数
D.f(x)的单调递增区间是 (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练2练习卷(解析版) 题型:填空题
我们把形如y= (a>0,b>0)的函数因其图象类似于汉字中的“囧”字,故生动地称为“囧函数”,若当a=1,b=1时的“囧函数”与函数y=lg|x|的交点个数为n,则n=________.
(a>0,b>0)的函数因其图象类似于汉字中的“囧”字,故生动地称为“囧函数”,若当a=1,b=1时的“囧函数”与函数y=lg|x|的交点个数为n,则n=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(解析版) 题型:选择题
设函数f(x)= 若f(a)+f(-1)=2,则a等于( ).
若f(a)+f(-1)=2,则a等于( ).
A.-3 B.±3 C.-1 D.±1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习7-2随机变量及其分布练习卷(解析版) 题型:选择题
甲射击命中目标的概率是 ,乙命中目标的概率是
,乙命中目标的概率是 ,丙命中目标的概率是
,丙命中目标的概率是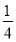 .现在三人同时射击目标,则目标被击中的概率为( ).
.现在三人同时射击目标,则目标被击中的概率为( ).
A. B.
B. C.
C. D.
D. 
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习6-2椭圆、双曲线、抛物线练习卷(解析版) 题型:选择题
已知直线l交椭圆4x2+5y2=80于M,N两点,椭圆与y轴的正半轴交于B点,若△BMN的重心恰好落在椭圆的右焦点上,则直线l的方程是( ).
A.6x-5y-28=0 B.6x+5y-28=0
C.5x+6y-28=0 D.5x-6y-28=0
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习6-1直线与圆练习卷(解析版) 题型:填空题
在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习5-1空间几何体与点等练习卷(解析版) 题型:解答题
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点.
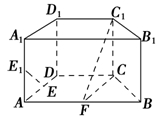
(1)证明:直线EE1∥平面FCC1;
(2)求二面角B-FC1-C的余弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习3-1三角函数与三角恒等变换练习卷(解析版) 题型:解答题
已知函数f(x)=cos cos
cos -sin xcos x+
-sin xcos x+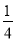
(1)求函数f(x)的最小正周期和最大值;
(2)求函数f(x)单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com