
| A. | ①②③ | B. | ①③④ | C. | ②③④ | D. | ①②④ |
分析 根据题意,画出函数f(x)的图象,结合函数的图象与解析式,对以下4个命题进行判断即可.
解答 解:由题意:x-{x}=x-m,
∴令g(x)=x-{x}=x-m,
当m=0时,-$\frac{1}{2}$<x$≤\frac{1}{2}$,∴g(x)=x,
当m=1时,1-$\frac{1}{2}$<x≤1+$\frac{1}{2}$,g(x)=x-1;
当m=2时,2$-\frac{1}{2}$<x≤2$+\frac{1}{2}$,g(x)=x-2;
…
…
画出函数的图象,如图所示: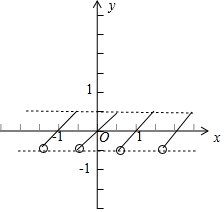
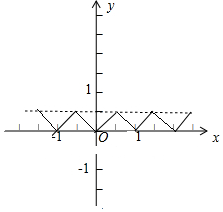
f(x)=|x-{x}|就是将g(x)关于x轴翻折到上方(图右).
由图象知
①函数y=f(x)的定义域为R,值域为$[0,\frac{1}{2}]$;正确.
②函数y=f(x)的图象关于直线$x=\frac{k}{2}(k∈Z)$对称;正确.
③函数y=f(x)在$[-\frac{1}{2},\frac{1}{2}]$上是增函数;不对;在$[-\frac{1}{2},0]$是减函数,$[0,\frac{1}{2}]$是增函数.
④对任意实数x,都有f(-x)=f(x)正确.
确的命题是①②④.
故选:D.
点评 本题考查了新定义的题目,解题的关键是读懂定义的内涵,尝试探究解决,是较难的题目.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [0,1] | C. | [0,1]∪(1,4] | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com