Question

15．已知函数f（x）=x³+ax+b（a，b∈R），且f（x）在x=$\frac{\sqrt{3e}}{3}$时取极小值0（其中e为自然对数的底数）．
（1）求a，b的值；
（2）记g（x）=（-a）^x，m、n是函数g（x）定义域内的任意值，且m≠n，判断g（$\frac{m+n}{2}$）、$\frac{g（m）+g（n）}{2}$、$\frac{g（m）-g（n）}{m-n}$的大小，并说明理由．

Answer 1

分析 （1）因为f（x）在x=$\frac{\sqrt{3}e}{3}$时取极小值0，所以$\left\{\begin{array}{l}{f（\frac{\sqrt{3}e}{3}）=0}\\{f'（\frac{\sqrt{3}e}{3}）=0}\end{array}\right.$，列出方程直接可求出；
（2）由题意g（x）=e^x，利用作差法与构造新函数h（x）=（x-2）e^x+x+2 （x＞0），利用函数单调性判断h（x）＞0即可；利用作商法求证$\frac{g（m）+g（n）}{2}$＞g（$\frac{m+n}{2}$）；利用数形结合方法推导 $\frac{g（m）-g（n）}{m-n}$＞g（$\frac{M+n}{2}$）．

解答 解：（1）因为f（x）在x=$\frac{\sqrt{3}e}{3}$时取极小值0，所以$\left\{\begin{array}{l}{f（\frac{\sqrt{3}e}{3}）=0}\\{f'（\frac{\sqrt{3}e}{3}）=0}\end{array}\right.$，
因为f（x）=x³+ax+b，所以f'（x）=3x²+a，
所以$（\frac{\sqrt{3}e}{3}）^{3}+\frac{\sqrt{3}e}{3}a+b=0$，
3$（\frac{\sqrt{3}e}{3}）^{2}+a$=0，
解得：a=-e，b=$\frac{2\sqrt{3e}e}{9}$．
（2）因为a=-e，所以g（x）=e^x，
所以$\frac{g（m）+g（n）}{2}=\frac{{e}^{m}+{e}^{n}}{2}$，
$\frac{g（m）-g（n）}{m-n}=\frac{{e}^{m}-{e}^{n}}{m-n}$，
设m＞n，此时$\frac{g（m）+g（n）}{2}＞0$，$\frac{g（m）-g（n）}{m-n}＞0$，
$\frac{g（m）+g（n）}{2}-\frac{g（m）-g（n）}{m-n}$
=$\frac{{e}^{m}+{e}^{n}}{2}$-$\frac{{e}^{m}-{e}^{n}}{m-n}$
=$\frac{{e}^{n}[（m-n-2）{e}^{m-n}+（m-n+2）]}{2（m-n）}$，
令h（x）=（x-2）e^x+x+2 （x＞0），
所以h'（x）=（x-1）e^x+1 （x＞0），
h''（x）=xe^x  （x＞0），
因为x＞0，所以h''（x）＞0，所以y=h'（x）在（0，+∞）上单调递增．
所以当x＞0时，h'（x）＞h'（0）=0，
所以y=h（x）在（0，+∞）上单调递增，
所以当x＞0时，h（x）＞h（0）=0，
又因为m＞n，
所以$\frac{g（m）+g（n）}{2}-\frac{g（m）-g（n）}{m-n}$＞0，
即$\frac{g（m）+g（n）}{2}$＞$\frac{g（m）-g（n）}{m-n}$；

令k（x）=$\frac{g（\frac{m+n}{2}）}{\frac{g（m）+g（n）}{2}}$=$\frac{2{e}^{\frac{m}{2}•}{e}^{\frac{n}{2}}}{{e}^{m}+{e}^{n}}$，
则$\frac{1}{k（x）}$=$\frac{{e}^{m}+{e}^{n}}{2{e}^{\frac{m}{2}•}{e}^{\frac{n}{2}}}$=$\frac{1}{2}$ （$\frac{{e}^{\frac{m}{2}}}{{e}^{\frac{n}{2}}}$+$\frac{{e}^{\frac{n}{2}}}{{e}^{\frac{m}{2}}}$）＞1，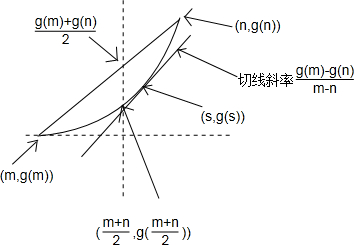
所以k（x）＜1⇒g（$\frac{m+n}{2}$）＜$\frac{g（m）+g（n）}{2}$；
因为g（x）=e^x是单调递增函数，所以$\frac{g（m）+g（n）}{2}$＞g（$\frac{m+n}{2}$）；
根据图象：
$\frac{g（m）-g（n）}{m-n}$ 是图中直角三角形斜边的斜率；
只有当s＞$\frac{m+n}{2}$时，才存在
g'（s）=$\frac{g（m）-g（n）}{m-n}$ 成立．
因为g（x）=g'（x）
所以$\frac{g（m）-g（n）}{m-n}=g（s）\\;＞\\;g（\frac{m+n}{2}）$＞g（$\frac{M+n}{2}$）

故：g（$\frac{m+n}{2}$）＜$\frac{g（m）-g（n）}{m-n}$＜$\frac{g（m）+g（n）}{2}$．

点评 本题主要考查了利用导数求函数的单调性与最值，以及作差与作商比较大小，数学结合思想等知识点，属中等偏上题．