
已知函数 在
在 与
与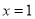 处都取得极值.
处都取得极值.
(1)求函数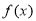 的解析式;
的解析式;
(2)求函数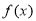 在区间[-2,2]的最大值与最小值.
在区间[-2,2]的最大值与最小值.
(1)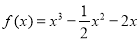 ;(2)
;(2)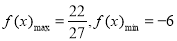 .
.
【解析】
试题分析:(1)由已知函数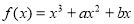 在
在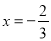 与
与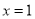 处都取得极值,得到
处都取得极值,得到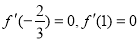 ,求出
,求出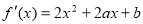 得到:关于a,b的两个方程,联立解方程组可得到a,b的值,从而可写出函数
得到:关于a,b的两个方程,联立解方程组可得到a,b的值,从而可写出函数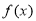 的解析式;(2)由(1)已求出
的解析式;(2)由(1)已求出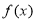 的解析式,要求函数
的解析式,要求函数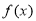 在区间[-2,2]的最大值与最小值,只需先求出函数
在区间[-2,2]的最大值与最小值,只需先求出函数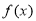 在区间[-2,2]的极大值与极小值,再求出两个端点的函数值,然后比较这四个数值的大小,得其中的最大者就是该函数的最大值,最小者就是该函数的最小值.
在区间[-2,2]的极大值与极小值,再求出两个端点的函数值,然后比较这四个数值的大小,得其中的最大者就是该函数的最大值,最小者就是该函数的最小值.
试题解析:(1)f(x)=x3+ax2+bx,f?(x)=3x2+2ax+b 1分
由f?(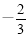 )=
)=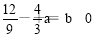 ,f?(1)=3+2a+b=0 3分
,f?(1)=3+2a+b=0 3分
得a=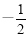 ,b=-2 5分
,b=-2 5分
经检验,a=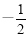 ,b=-2符合题意
,b=-2符合题意
所以,所求的函数解析式为: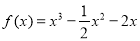 6分
6分
(2)由(1)得f?(x)=3x2-x-2=(3x+2)(x-1), 7分
列表如下:
x | (-2,- | - | (- | 1 | (1,2) |
f?(x) | + | 0 | - | 0 | + |
f(x) | ? | 极大值 | ? | 极小值 | ? |
9分
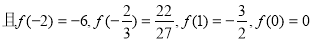 11分
11分
所以当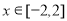 时,
时,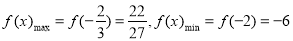 12分
12分
考点:1.函数导数;2.函数极值;3.函数最值.


科目:高中数学 来源:2015届福建漳州实验中学高二(上)期末考试文科数学试卷(解析版) 题型:选择题
对于任意给定的实数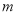 ,直线
,直线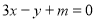 与双曲线
与双曲线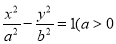 ,
,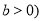 最多有一个交点,则双曲线的离心率等于( )
最多有一个交点,则双曲线的离心率等于( )
A.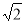 B.
B.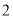 C.
C.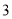 D.
D.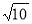
查看答案和解析>>
科目:高中数学 来源:2015届甘肃省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
如图,过圆内接四边形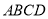 的顶点
的顶点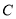 引圆的切线
引圆的切线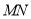 ,
,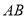 为圆直径,若∠
为圆直径,若∠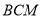 =
=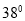 ,则∠
,则∠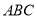 =( )
=( )

A.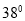 B.
B.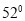 C.
C.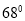 D.
D.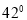
查看答案和解析>>
科目:高中数学 来源:2015届甘肃省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
在各项都为正数的等比数列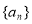 中,首项为3,前3项和为21,则
中,首项为3,前3项和为21,则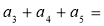 ( )
( )
A.33 B.72 C.84 D.189
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com