
分析 (1)求出直线AB的方程,利用圆的圆心到直线的距离与半径半弦长的关系推出结果即可.
(2)法1:设点P的坐标为(x,y),若P、M、C三点不共线时,得到|CM|2=|MP|2+|CP|2,的轨迹方程,若P、M重合时,即P(-3,-3),验证结果.推出结论.
法2:设点P的坐标为(x,y),当x≠0且x≠-3时,通过kCP•kAB=-1,求解点P的轨迹方程.
法3:设点P的坐标为(x,y),通过$\overrightarrow{CP}•\overrightarrow{MP}=0$,得到点P的轨迹方程.
解答 解:(1)由题意得,圆心C(0,-2),半径r=5.
当α=135°时,直线AB的斜率k=tan135°=-1,…(2分)
∴直线AB的方程为:y+3=-(x+3),即x+y+6=0,
∴圆心C到直线AB的距离为:$d=\frac{|0-2+6|}{{\sqrt{2}}}=2\sqrt{2}$,…(4分)
由垂径定理得,$|AB|=2\sqrt{{r^2}-{d^2}}=2\sqrt{25-8}=2\sqrt{17}$.…(6分)
(2)法1:设点P的坐标为(x,y),…(7分)
若P、M、C三点不共线时,则|CM|2=|MP|2+|CP|2,…(9分)
即10=(x+3)2+(y+3)2+x2+(y+2)2,
化简得,x2+y2+3x+5y+6=0. (*) …(11分)
若P、M重合时,即P(-3,-3),则(-3)2+(-3)2-9-15+6=9+9-9-15+6=0也满足上述方程(*)…12分. …(12分)
若P、C重合时,即P(0,-2),则02+(-2)2+0-10+6=0也满足上述方程(*). …(13分)
综上所述,点P的轨迹方程为x2+y2+3x+5y+6=0(或${(x+\frac{3}{2})^2}+{(y+\frac{5}{2})^2}=\frac{5}{2}$).…(14分)
法2:设点P的坐标为(x,y),…(7分)
当x≠0且x≠-3时,由题意有,CP⊥AB,则kCP•kAB=-1,…(9分)
又${k_{CP}}=\frac{y+2}{x}$,${k_{AB}}={k_{PM}}=\frac{y+3}{x+3}$,
∴$\frac{y+2}{x}•\frac{y+3}{x+3}=-1$,化简得,x2+y2+3x+5y+6=0,(*) …(11分)
当x=0或x=-3时,点P(0,-3)或P(0,-2)或P(-3,-2)或P(-3,-3)均满足方程.(13分)
所以点P的轨迹方程为x2+y2+3x+5y+6=0. …(14分)
法3:设点P的坐标为(x,y),…(7分)
由题意有,$\overrightarrow{CP}⊥\overrightarrow{MP}$,则$\overrightarrow{CP}•\overrightarrow{MP}=0$,…(9分)
∵$\overrightarrow{CP}=(x,y+2)$,$\overrightarrow{MP}=(x+3,y+3)$,…(10分)
∴x(x+3)+(y+2)(y+3)=0,化简得x2+y2+3x+5y+6=0,…(13分)
所以点P的轨迹方程为x2+y2+3x+5y+6=0.…(14分)
点评 本题考查直线与圆的位置关系的综合应用,轨迹方程的求法,考查分析问题解决问题的能力.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校高三文,理各两个班在11月份进行了一次质量考试,考生成绩情况如下表所示:已知用分层抽样方法在分数[400,480)的考生中随机抽取27名考生进行质量分析,其中文科考生抽取了7名.(1)求a的值(2)如图是文科不低于550分的5名考生的语文成绩(其中语文满分为150分)的茎叶图,请计算这5名考生的语文成绩的方差;(3)在成绩不低于550分的所有考生中抽取2名进行治疗分析,求至少抽到一名理科生的概率.
某校高三文,理各两个班在11月份进行了一次质量考试,考生成绩情况如下表所示:已知用分层抽样方法在分数[400,480)的考生中随机抽取27名考生进行质量分析,其中文科考生抽取了7名.(1)求a的值(2)如图是文科不低于550分的5名考生的语文成绩(其中语文满分为150分)的茎叶图,请计算这5名考生的语文成绩的方差;(3)在成绩不低于550分的所有考生中抽取2名进行治疗分析,求至少抽到一名理科生的概率. | [0,400] | [400,480] | [480,550] | [550,750] | |
| 文科考生 | 67 | 35 | 19 | 5 |
| 理科考生 | 53 | a | 41 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
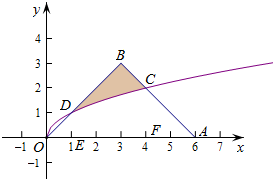 如图,等腰三角形OAB的顶点A、B的坐标分别为(6,0),(3,3),且AB与曲线y=$\sqrt{x}$交于点C,在△OAB中任取一点P,则点P落在阴影部分的概率为( )
如图,等腰三角形OAB的顶点A、B的坐标分别为(6,0),(3,3),且AB与曲线y=$\sqrt{x}$交于点C,在△OAB中任取一点P,则点P落在阴影部分的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{27}$ | D. | $\frac{11}{54}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3360 | B. | -1120 | C. | -3360 | D. | 1120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com