
| 中年人 | 老年人 | 总计 | |
| 了解 | 40 | 20 | 60 |
| 不了解 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(k2≥kn) | 0.050 | 0.010 | 0.001 |
| kn | 3.841 | 6.635 | 10.828 |
分析 (1)计算K2,验证K2是否大于6.635即可得出结论;
(2)分别求出X所有可能取值的概率,得出X的分布列,计算数学期望.
解答 解:(1)K2=$\frac{110×(40×30-20×20)^{2}}{60×50×60×50}$≈7.822>6.635.
∴有99%的把握认为是否了解“医药互联网+”与年龄段有关.
(2)从中年人中随机抽取1位,则此人了解“医药互联网+”的概率为$\frac{40}{60}$=$\frac{2}{3}$.
随机变量X的可能取值为0,1,2,3,4,5,6.
P(X=0)=($\frac{1}{3}$)6=$\frac{1}{{3}^{6}}$,P(X=1)=${C}_{6}^{1}$($\frac{1}{3}$)5($\frac{2}{3}$)=$\frac{4}{{3}^{5}}$,P(X=2)=${C}_{6}^{2}$($\frac{2}{3}$)2($\frac{1}{3}$)4=$\frac{20}{{3}^{5}}$,P(X=3)=${C}_{6}^{3}$($\frac{2}{3}$)3($\frac{1}{3}$)3=$\frac{160}{{3}^{6}}$,
P(X=4)=${C}_{6}^{4}$($\frac{2}{3}$)4($\frac{1}{3}$)2=$\frac{80}{{3}^{5}}$,P(X=5)=${C}_{6}^{5}$($\frac{2}{3}$)5($\frac{1}{3}$)=$\frac{64}{{3}^{5}}$,P(X=6)=($\frac{2}{3}$)6=$\frac{64}{{3}^{6}}$.
X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| P | $\frac{1}{{3}^{6}}$ | $\frac{4}{{3}^{5}}$ | $\frac{20}{{3}^{5}}$ | $\frac{160}{{3}^{6}}$ | $\frac{80}{{3}^{5}}$ | $\frac{64}{{3}^{5}}$ | $\frac{64}{{3}^{6}}$ |
点评 本题考查了独立性检验的应用,随机变量的分布列和数学期望,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
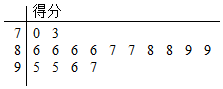 某校就开展“学习习惯养成”教育活动的情况进行调查,随机抽取了16名学生进行测试,用“10分制”以茎叶图方式记录了他们的测试分数(如图),若所得分数不低于9.5分,则称该学生“学习习惯非常好”.
某校就开展“学习习惯养成”教育活动的情况进行调查,随机抽取了16名学生进行测试,用“10分制”以茎叶图方式记录了他们的测试分数(如图),若所得分数不低于9.5分,则称该学生“学习习惯非常好”.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | t | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
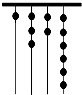 远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”,如图所示的是一位母亲记录的孩子自出生后的天数,在从右向左依次排列的不同绳子上打结,满七进一,根据图示可知,孩子已经出生的天数是( )
远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”,如图所示的是一位母亲记录的孩子自出生后的天数,在从右向左依次排列的不同绳子上打结,满七进一,根据图示可知,孩子已经出生的天数是( )| A. | 336 | B. | 510 | C. | 1326 | D. | 3603 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com