练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．在回归分析与独立性检验中：
    ①相关关系是一种确定关系  
    ②在回归模型中，x称为解释变量，y称为预报变量  
    ③R2越接近于1，表示回归的效果越好  
    ④在独立性检验中，|ad-bc|越大，两个分类变量关系越弱；|ad-bc|越小，两个分类变量关系越强  
    ⑤残差点比较均匀地落在水平的带状区域中，带状区域宽度越窄，回归方程的预报精度越高，
    正确命题的个数为（　　）
    A．5B．4C．3D．2

    分析 根据独立性检验与线性相关关系的应用问题，对选项中的命题进行分析、判断正误即可．

    解答 解：对于①，相关关系是一种不确定关系，∴①错误；  
    对于②，在回归模型中，x称为解释变量，y称为预报变量，∴②正确；  
    对于③，R2越接近于1，表示回归的效果越好，③正确；  
    对于④，在独立性检验中，|ad-bc|越大，观测值K2就越大，
    两个分类变量关系越强；|ad-bc|越小，K2就越小，两个分类变量关系越弱，④错误；  
    对于⑤，残差点比较均匀地落在水平的带状区域中，带状区域宽度越窄，回归方程的预报精度越高，⑤正确．
    综上，正确命题的序号是②③⑤，共3个．
    故选：C．

    点评 本题考查了线性回归分析语独立性检验的应用问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    6．已知F为抛物线C：y2=4x的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于A、B两点，直线l2与C交于D、E两点，则|AB|+|DE|的最小值为（　　）
    A．16B．14C．12D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．若x=-2是函数f（x）=（x2+ax-1）ex-1的极值点，则f（x）的极小值为（　　）
    A．-1B．-2e-3C．5e-3D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．设数列{an}满足a1=2，an+1=2an+2n+1（n∈N*）．
    （1）若bn=$\frac{{a}_{n}}{{2}^{n}}$，证明：数列{bn}为等差数列，并求出数列{bn}的通项公式；
    （2）若cn=an+bn，求数列{cn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知△ABC的面积为$5\sqrt{3}，A=\frac{π}{6}，AB=5$，则BC=$\sqrt{13}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．过直线x-y-2=0上的动点P作抛物线y=$\frac{1}{2}$x2的切线，切点分别为M，N，则直线MN过点（1，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

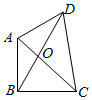    12．如图，已知平面四边形ABCD，AB⊥BC，AB=BC=AD=2，CD=3，AC与BD交于点O，记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$，I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$，I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$，则（　　）
    A．I1＜I2＜I3B．I1＜I3＜I2C．I3＜I1＜I2D．I2＜I1＜I3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．设函数y=$\sqrt{4-{x}^{2}}$的定义域为A，函数y=ln（1-x）的定义域为B，则A∩B=（　　）
    A．（1，2）B．（1，2]C．（-2，1）D．[-2，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．设x∈R，则“2-x≥0”是“|x-1|≤1”的（　　）
    A．充分而不必要条件B．必要而不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    同步练习册答案