
分析 (1)首先判断出函数f(x)=ax2-2x+1在区间[1,3]上为单调减函数,然后求出M(a)、N(a),进而求出g(a)的表达式即可;
(2)由一次函数的性质知,g(a)=-8a+4在区间(0,$\frac{1}{3}$]单调减,a为$\frac{1}{2}$时,g(a)取最小值,代入求解即可.
解答 解:(1)∵$\frac{1}{3}≤a≤1$,
∴f(x)的图象为开口向上的抛物线,且对称轴$x=\frac{1}{a}∈[1,3]$.
∴f(x)有最小值$N(a)=1-\frac{1}{a}$.
当2≤$\frac{1}{a}$≤3时,a∈[$\frac{1}{3},\frac{1}{2}],f(x)$有最大值M(a)=f(1)=a-1;
当1≤$\frac{1}{a}$<2时,a∈($\frac{1}{2},1],f(x)$有最大值M(a)=f(3)=9a-5;
∴$g(a)=\left\{\begin{array}{l}a-2+\frac{1}{a}(\frac{1}{3}≤a≤\frac{1}{2})\\ 9a-6+\frac{1}{a}(\frac{1}{2}<a≤1).\end{array}\right.$
(2)设$\frac{1}{3}≤{a_1}<{a_2}≤\frac{1}{2}$,
则 $g({a_1})-g({a_2})=({a_1}-{a_2})(1-\frac{1}{{{a_1}{a_2}}})>0$,
∴g(a1)>g(a2),
∴$g(a)在[\frac{1}{3},\frac{1}{2}]$上是减函数.
设$\frac{1}{2}<{a_1}<{a_2}≤1$,
则$g({a_1})-g({a_2})=({a_1}-{a_2})(9-\frac{1}{{{a_1}{a_2}}})<0$,
∴g(a1)<g(a2),
∴g(a)在($\frac{1}{2}$,1]上是增函数
∴当$a=\frac{1}{2}$时,g(a)有最小值$\frac{1}{2}$.
点评 本题主要考查了二次函数的性质及其运用,考查了函数的表达式以及最值的求法,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (2,3] | B. | (2,3) | C. | [2,3] | D. | (2,6] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
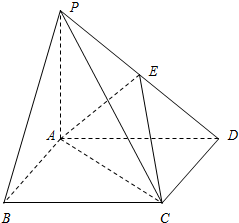 如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com