
分析 (Ⅰ)求出函数的导数,通过讨论m的范围,求出函数的单调区间,结合题意确定m的范围即可;
(Ⅱ)问题等价于(x-2)ex-mx3+x+2≥0,由题意知当x∈[0,+∞),不等式(x-2)ex-mx3+x+2≥0恒成立.令h(x)=(x-2)ex-mx3+x+2,根据函数的单调性求出m的范围即可.
解答 解:(Ⅰ)f′(x)=(mx3+3mx2-x-3),
①当m≤0时,若x∈(2,3),则f'(x)<0,
所以函数f(x)在(2,3)上单调递减,不满足题意;
②当m>0时,由f'(x)=0,得x=-3或$x=\sqrt{\frac{1}{m}}$或$x=-\sqrt{\frac{1}{m}}$,
易知f(x)在$(0,\sqrt{\frac{1}{m}})$上单调递减,在$(\sqrt{\frac{1}{m}},+∞)$上单调递增.
因为f(x)在区间(2,3)上不是单调函数,
所以$2<\sqrt{\frac{1}{m}}<3$,解得$\frac{1}{9}<m<\frac{1}{4}$.
综上所述,实数m的取值范围是$(\frac{1}{9},\frac{1}{4})$.
(Ⅱ)不等式$\frac{f(x)}{{{e^{2x}}}}+2≤x$等价于$\frac{{m{x^3}-x-2}}{{{e^{2x}}}}+2≤x$,
等价于(x-2)ex-mx3+x+2≥0,
由题意知当x∈[0,+∞),不等式(x-2)ex-mx3+x+2≥0恒成立.
令h(x)=(x-2)ex-mx3+x+2,
则h'(x)=(x-1)ex-3mx2+1,
令ϕ(x)=h'(x)=(x-1)ex-3mx2+1,
由ϕ(0)=h'(0)=0,且ϕ'(x)=x(ex-6m).
①当6m≤1,即$m≤\frac{1}{6}$时,由x≥0,知ex≥1,
则ϕ'(x)=x(ex-6m)≥0,
所以函数ϕ(x)即h'(x)在[0,+∞)上单调递增.
又由ϕ(0)=h'(0)=0,
故当x∈[0,+∞)时,h'(x)≥h'(0)=0,
所以h(x)在[0,+∞)上单调递增.
又因为h(0)=0,所以h(x)≥0在[0,+∞)上恒成立,满足题意;
②当6m>1,即$m>\frac{1}{6}$时,
若x∈(0,ln(6m)),则ϕ'(x)=x(ex-6m)<0,
函数ϕ(x)即h'(x)单调递减,
又由ϕ(0)=h'(0)=0,
所以当x∈(0,ln(6m))时,h'(x)<h'(0)=0,
所以h(x)在(0,ln(6m))上单调递减.
又因为h(0)=0,所以x∈(0,ln(6m))时,h(x)<0,
这与题意h(x)≥0在[0,+∞)上恒成立相矛盾,故舍去.
综上所述,$m≤\frac{1}{6}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道综合题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | cosx+2 | B. | -cosx-2 | C. | cosx-2 | D. | -cosx+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{1}{3}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
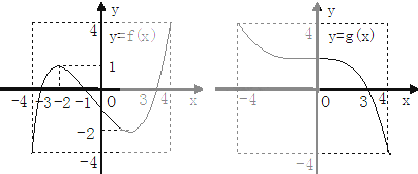
| A. | 方程f[g(x)]=0有且仅有三个根 | B. | 方程g[f(x)]=0有且仅有三个根 | ||
| C. | 方程f[f(x)]=0有且仅有两个根 | D. | 方程g[g(x)]=0有且仅有两个根 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<a<1 | B. | $\frac{1}{16}$≤a<1 | C. | a>1 | D. | 0<a≤$\frac{1}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com