
如图所示,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1、OF2的中点分别为B1、B2,且△AB1B2是面积为4的直角三角形.
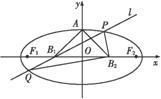
(1)求该椭圆的离心率和标准方程;
(2)过B1作直线交椭圆于P、Q两点,使PB2⊥QB2,求△PB2Q的面积.
解:(1)设椭圆的标准方程为 +
+ =1(a>b>0),焦距为2c,则A(0,b),|OB1|=|OB2|=
=1(a>b>0),焦距为2c,则A(0,b),|OB1|=|OB2|=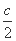 .
.
由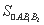 =4得
=4得 ·c·b=4,
·c·b=4,
即bc=8.①
又△AB1B2是直角三角形,
且|OB1|=|OB2|,∴b=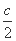 .②
.②
由①②可得b=2,c=4.
∴a2=20.
∴椭圆的标准方程为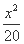 +
+ =1,离心率e=
=1,离心率e= =
=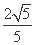 .
.
(2)由(1)知B1(-2,0),B2(2,0).
由题意知,直线PQ的倾斜角不为0,
故可设直线PQ的方程为x=my-2.
代入椭圆方程得(m2+5)y2-4my-16=0.(*)
设P1(x1,y1),P2(x2,y2),
则y1,y2是方程(*)的两根.
∴y1+y2=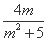 ,y1·y2=-
,y1·y2=- .
.
又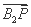 =(x1-2,y1),
=(x1-2,y1),  =(x2-2,y2).
=(x2-2,y2).
∴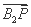 ·
· =(x1-2)(x2-2)+y1y2
=(x1-2)(x2-2)+y1y2
=(my1-4)(my2-4)+y1y2
=(m2+1)y1y2-4m(y1+y2)+16
=-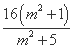 -
-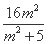 +16
+16
=-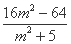 .
.
由PB2⊥B2Q知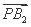 ·
· =0,
=0,
即-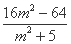 =0,
=0,
16m2-64=0,解得m=±2.
当m=2时,y1+y2=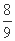 ,y1y2=-
,y1y2=-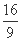 ,
,
|y1-y2|=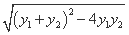 =
=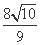 .
.
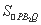 =
= |B1B2|·|y1-y2|=
|B1B2|·|y1-y2|=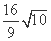 .
.
当m=-2时,由椭圆的对称性可得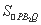 =
=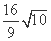 .
.
综上所述,△PB2Q的面积为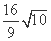 .
.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
已知F1、F2为双曲线C:x2-y2=2的左、右焦点,点P在C上,|PF1|=2|PF2|,则cos∠F1PF2=( )
(A)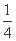 (B)
(B)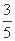 (C)
(C)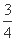 (D)
(D)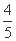
查看答案和解析>>
科目:高中数学 来源: 题型:
若点P是以A(- ,0),B(
,0),B( ,0)为焦点,实轴长为2
,0)为焦点,实轴长为2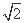 的双曲线与圆x2+y2=10的一个交点,则|PA|+|PB|的值为( )
的双曲线与圆x2+y2=10的一个交点,则|PA|+|PB|的值为( )
(A)2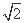 (B)4
(B)4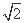 (C)4
(C)4 (D)6
(D)6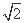
查看答案和解析>>
科目:高中数学 来源: 题型:
椭圆 +
+ =1(a>b>0)的左、右顶点分别是A、B,左、右焦点分别是F1、F2,若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为( )
=1(a>b>0)的左、右顶点分别是A、B,左、右焦点分别是F1、F2,若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为( )
(A) (B)
(B) (C)
(C) (D)
(D)  -2
-2
查看答案和解析>>
科目:高中数学 来源: 题型:
设椭圆 +
+ =1(a>b>0)的左焦点为F,离心率为
=1(a>b>0)的左焦点为F,离心率为 ,过点F且与x轴垂直的直线被椭圆截得的线段长为
,过点F且与x轴垂直的直线被椭圆截得的线段长为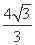 .
.
(1)求椭圆的方程;
(2)设A,B分别为椭圆的左、右顶点,过点F且斜率为k的直线与椭圆交于C,D两点.若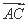 ·
·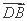 +
+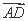 ·
·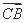 =8,求k的值.
=8,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知A、B分别为椭圆 +
+ =1(a>b>0)的左、右顶点,C(0,b),直线l:x=2a与x轴交于点D,与直线AC交于点P,若∠DBP=
=1(a>b>0)的左、右顶点,C(0,b),直线l:x=2a与x轴交于点D,与直线AC交于点P,若∠DBP= ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )
(A) (B)
(B) (C)
(C)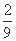 (D)
(D)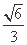
查看答案和解析>>
科目:高中数学 来源: 题型:
已知双曲线C1:  -
- =1(a>0,b>0)的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
=1(a>0,b>0)的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
(A)x2= y (B)x2=
y (B)x2= y
y
(C)x2=8y (D)x2=16y
查看答案和解析>>
科目:高中数学 来源: 题型:
某雷达测速区规定:凡车速大于或等于80 km/h的汽车视为“超速”,并将受到处罚.如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率分布直方图,则从图中可以看出被处罚的汽车大约有( )
A.20辆 B.40辆 C.60辆 D.80辆

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com