Question

12．棱长为1的正方体ABCD-A₁B₁C₁D₁的8个顶点都在球O的表面上，E，F分别为棱AB，A₁D₁的中点，则经过E，F球的截面面积的最小值为（　　）

• A． $\frac{3}{8}$π
• B． $\frac{π}{2}$
• C． $\frac{5}{8}$π
• D． $\frac{7}{8}$π

Answer 1

分析 先求球的半径，再求EF，球心到截面圆的距离，OP，然后求出截面圆的半径，就是图中QP即可得出结论．

解答 解：因为正方体内接于球，所以2R=$\sqrt{{1}^{2}+{1}^{2}+{1}^{1}}$=$\sqrt{3}$，R=$\frac{\sqrt{3}}{2}$，
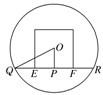
过球心O和点E、F的大圆的截面图如图所示，
则直线被球截得的线段为QR，过点O作OP⊥QR，垂足为点P，EF=$\frac{\sqrt{6}}{2}$，OF=$\frac{\sqrt{2}}{2}$
OP=$\sqrt{（\frac{\sqrt{2}}{2}）^{2}-（\frac{\sqrt{6}}{4}）^{2}}$=$\frac{\sqrt{2}}{4}$，
所以，在△QPO中，QP=$\sqrt{（\frac{\sqrt{3}}{2}）^{2}-（\frac{\sqrt{2}}{4}）^{2}}$=$\frac{\sqrt{10}}{4}$．
所以所求经过E、F的平面截球O所得的截面的面积的最小值是：$π•（\frac{\sqrt{10}}{4}）^{2}$=$\frac{5}{8}π$．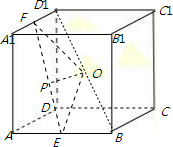

故选：C．

点评 本题考查组合体的结构特征，球的内接多面体，截面圆的面积，考查空间想象能力，计算能力，是中档题．