
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
分析 S=(x-a)2+(lnx-$\frac{{a}^{2}}{4}$)2(a∈R),其几何意义为两点(x.lnx),(a,$\frac{{a}^{2}}{4}$)的距离的平方,由y=lnx的导数为y′=$\frac{1}{x}$,得k=$\frac{1}{{x}_{1}}$,由点(a,$\frac{{a}^{2}}{4}$)在曲线y=$\frac{1}{4}$x2上,得k=$\frac{1}{2}$x2,令f(x)=lnx,g(x)=$\frac{1}{4}{x}^{2}$,则D(x)=$\sqrt{({x}_{1}-{x}_{2})^{2}+[f({x}_{1})-g({x}_{2})]^{2}}$+g(x2)+1,而g(x2)+1是抛物线y=$\frac{1}{4}{x}^{2}$上的点到准线y=-1的距离,从而D可以看作抛物线上的点(x2,g(x2))到焦点距离和到f(x)=lnx上的点的距离的和,D的最小值是点F(0,1)到f(x)=lnx上的点的距离的最小值.
解答 解:S=(x-a)2+(lnx-$\frac{{a}^{2}}{4}$)2(a∈R),其几何意义为: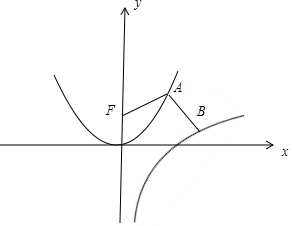
两点(x.lnx),(a,$\frac{{a}^{2}}{4}$)的距离的平方,
由y=lnx的导数为y′=$\frac{1}{x}$,∴k=$\frac{1}{{x}_{1}}$
点(a,$\frac{{a}^{2}}{4}$)在曲线y=$\frac{1}{4}$x2上,
∴y′=$\frac{1}{2}$x,∴k=$\frac{1}{2}$x2,
令f(x)=lnx,g(x)=$\frac{1}{4}{x}^{2}$,
则D(x)=$\sqrt{({x}_{1}-{x}_{2})^{2}+[f({x}_{1})-g({x}_{2})]^{2}}$+g(x2)+1,
而g(x2)+1是抛物线y=$\frac{1}{4}{x}^{2}$上的点到准线y=-1的距离,
即抛物线y=$\frac{1}{4}{x}^{2}$上的点到焦点(0,1)的距离,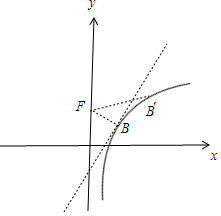
则D可以看作抛物线上的点(x2,g(x2))到焦点距离和到f(x)=lnx上的点的距离的和,
即|AF|+|AB|,
由两点之间线段最短,得D的最小值是点F(0,1)到f(x)=lnx上的点的距离的最小值,
由点到直线上垂线段最短,这样就最小,
即取B(x0,lnx0),
则${f}_{'}({x}_{0})•\frac{ln{x}_{0}}{{x}_{0}}$=-1,垂直,
则$ln{x}_{0}-1=-{{x}_{0}}^{2}$,解得x0=1,
∴F到B(1,0)的距离就是点F(0,1)到f(x)=lnx上的点的距离的最小值,
∴D的最小值为|DF|=$\sqrt{2}$.
故选:C.
点评 本题考查函数的最小值的求法,考查导数、抛物线、两点间距离、点到直线距离等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、函数与方程思想,考查创新意识、应用意识,是中档题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 3 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
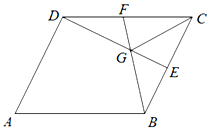 如图,边长为2的菱形ABCD中,∠A=60°,E、F分别是BC、DC的中点,G为 BF、DE的交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$.
如图,边长为2的菱形ABCD中,∠A=60°,E、F分别是BC、DC的中点,G为 BF、DE的交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30 | B. | 40 | C. | 50 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,1)∪[4,7) | B. | (-2,1]∪[4,7] | C. | (-2,1]∪(4,7) | D. | (-2,1]∪[4,7) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{2}}}{8}$ | D. | $\frac{{\sqrt{2}}}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com