【答案】
分析:由题设可先将3
x看作一个整体,将方程整理为一元二次方程,由根与系数的关系得到3
x1•3
x2=4,即可得到x
1+x
2=2log
32,进而再得到x
1x
2≤(log
32)
2.代入即可求得
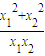
的最小值
解答:解:原方程可化为(3
x)
2-(4+a)•3
x+4=0,
∴3
x1•3
x2=4,
∴x
1+x
2=2log
32,
又(x
1+x
2)
2≥4x
1x
2,
∴x
1x
2≤(log
32)
2.
∴
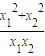
=
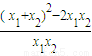
=
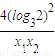
-2≥2.
故答案为2
点评:本题考查根与系数的关系,基本不等式在最值问题中的运用,指数型复合函数的应用,本题具有一定的探究性,思维量大,考查了转化化归的思想与推理判断的能力,解答的关键是将内层函数看作一个整体,及结合基本不等式求出x
1x
2≤(log
32)
2.

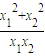 的最小值是 .
的最小值是 . 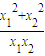 的最小值
的最小值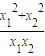 =
=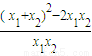 =
=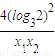 -2≥2.
-2≥2.
