
分析 (Ⅰ)求出f(x)的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)求出函数的导数,问题转化为a≥$\frac{{-x}^{2}+x}{lnx}$在(1,+∞)恒成立,令h(x)=$\frac{{-x}^{2}+x}{lnx}$,根据函数的单调性求出a的范围即可.
解答 解:(Ⅰ)f′(x)=$\frac{a}{x}$+2x-1=$\frac{{2x}^{2}-x+a}{x}$,(x>0),
令g(x)=2x2-x+a=2${(x-\frac{1}{4})}^{2}$+a-$\frac{1}{8}$,(x>0),
a≥$\frac{1}{8}$时,g(x)≥0,即f′(x)≥0,
f(x)在(0,+∞)递增,
0<a<$\frac{1}{8}$时,令g′(x)>0,解得:x>$\frac{1+\sqrt{1-8a}}{2}$或0<x<$\frac{1-\sqrt{1-8a}}{2}$,
令g′(x)<0,解得:$\frac{1-\sqrt{1-8a}}{2}$<x<$\frac{1+\sqrt{1-8a}}{2}$,
故f(x)在(0,$\frac{1-\sqrt{1-8a}}{2}$)递增,在($\frac{1-\sqrt{1-8a}}{2}$,$\frac{1+\sqrt{1-8a}}{2}$)递减,
在($\frac{1+\sqrt{1-8a}}{2}$,+∞)递增;
(Ⅱ)x=1时,显然成立,
x>1时,问题转化为a≥$\frac{{-x}^{2}+x}{lnx}$在(1,+∞)恒成立,
令h(x)=$\frac{{-x}^{2}+x}{lnx}$,则h′(x)=$\frac{(-2x+1)lnx+x-1}{{(lnx)}^{2}}$,
令m(x)=(-2x+1)lnx+x-1,(x>1),
则m′(x)=-2lnx+$\frac{1-x}{x}$<0,
故m(x)<m(1)=0,
故h′(x)在(1,+∞)递减,
而$\underset{lim}{x→1}$$\frac{{-x}^{2}+x}{lnx}$=$\underset{lim}{x→1}$$\frac{-2x+1}{\frac{1}{x}}$=-1,
故a≥-1.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,考查函数恒成立问题,是一道中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
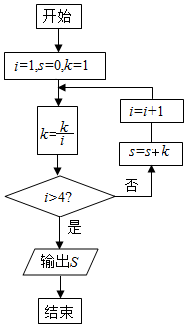 阅读如图的程序框图,运行相应的程序,则输出的S的值为( )
阅读如图的程序框图,运行相应的程序,则输出的S的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{41}{24}$ | D. | $\frac{103}{60}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3} | B. | {4,5} | C. | {1,3,4,5,6} | D. | {2,3,4,5,7} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{3}{2}$ | B. | ±$\frac{2}{3}$ | C. | ±$\frac{3}{4}$ | D. | ±$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
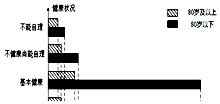 我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表:
我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com