
分析 (Ⅰ)当k=1时,f(x)=xlnx+1,f′(x)=lnx+1,由此利用导数性质能求出f(x)的单调区间.
(Ⅱ)由f(x)>0恒成立,得xlnx+(1-k)x+k>0,推导出k<$\frac{xlnx+x}{x-1}$恒成立,设g(x)=$\frac{xlnx+x}{x-1}(x>1)$,则g′(x)=$\frac{-lnx+x-2}{(x-1)^{2}}$,令μ(x)=-lnx+x-2,则${μ}^{'}(x)=-\frac{1}{x}+1=\frac{x-1}{x}$,由此利用导数秘技能求出k的最大整数值.
解答 解:(Ⅰ)当k=1时,f(x)=xlnx+1,
∴f′(x)=lnx+1,
由f′(x)>0,得x>$\frac{1}{e}$;由f′(x)<0,得0<x<$\frac{1}{e}$,
∴f(x)的单调递增区间为($\frac{1}{e}$,+∞),单调减区间为(0,$\frac{1}{e}$).
(Ⅱ)由f(x)>0恒成立,得xlnx+(1-k)x+k>0,
∴(x-1)k<xlnx+x,
∵x>1,∴k<$\frac{xlnx+x}{x-1}$恒成立,
设g(x)=$\frac{xlnx+x}{x-1}(x>1)$,则g′(x)=$\frac{-lnx+x-2}{(x-1)^{2}}$,
令μ(x)=-lnx+x-2,则${μ}^{'}(x)=-\frac{1}{x}+1=\frac{x-1}{x}$,
∵x>0,∴μ′(x)>0,μ(x)在(1,+∞)上单调递增,
而μ(3)=1-ln3<0,μ(4)=2-ln4>0,
∴存在x0∈(3,4),使μ(x0)=0,即x0-2=lnx0,
∴当x∈(x0,+∞)时,g′(x)<0,此时函数g(x)单调递减,
当x∈(x0,+∞)时,g′(x0)>0,此时函数g(x)单调递增,
∴g(x)在x=x0处有极小值(也是最小值),
∴$g(x)_{min}=g({x}_{0})=\frac{{x}_{0}ln{x}_{0}+{x}_{0}}{{x}_{0}-1}$=$\frac{{x}_{0}({x}_{0}-2)+{x}_{0}}{{x}_{0}-1}$=x0∈(3,4),
又由k<g(x)恒成立,即k<g(x)min=x0,
∴k的最大整数值为3.
点评 本题考查函数的单调区间的求法,考查实数的最大整数值的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
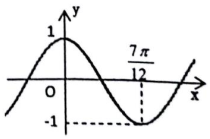 设函数y=sinωx(ω>0)的最小正周期是T,将其图象向左平移$\frac{1}{4}$T后,得到的图象如图所示,则函数y=sinωx(ω>0)的单增区间是( )
设函数y=sinωx(ω>0)的最小正周期是T,将其图象向左平移$\frac{1}{4}$T后,得到的图象如图所示,则函数y=sinωx(ω>0)的单增区间是( )| A. | [$\frac{7kπ}{6}$-$\frac{7π}{24}$,$\frac{7kπ}{6}$+$\frac{7π}{24}$](k∈Z) | B. | [$\frac{7kπ}{3}$-$\frac{7π}{24}$,$\frac{7kπ}{3}$+$\frac{7π}{24}$](k∈Z) | ||
| C. | [$\frac{7kπ}{3}$-$\frac{7π}{12}$,$\frac{7kπ}{3}$+$\frac{7π}{12}$](k∈Z) | D. | [$\frac{7kπ}{6}$+$\frac{7π}{24}$,$\frac{7kπ}{6}$+$\frac{21π}{24}$](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
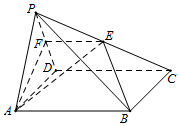 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com